المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Abel,s Integral |
 1910
 02:23 مساءً
date: 12-8-2018 |
Author : Sloane, N. J. A 
Book or Source : Sequence A102047 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 20-8-2018
3030
Date: 31-7-2019
2739
Date: 29-9-2018
1862
|
Abel's integral is the definite integral
 |
 |
 |
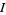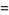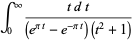(1) |
 |
 |
 |
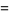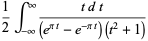(2) |
 |
 |
 |
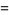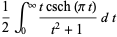(3) |
 |
 |
 |
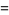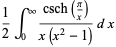(4) |
 |
 |
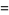![1/(pi^2)int_0^1(lnxdx)/((x^2-1)[((lnx)/pi)^2+1])](http://mathworld.wolfram.com/images/equations/AbelsIntegral/Inline15.gif) |
(5) |
 |
 |
 |
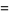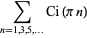(6) |
 |
 |
 |
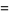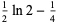(7) |
 |
 |
 |
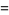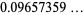(8) |
(OEIS A102047), where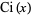 
is a cosine integral.
REFERENCES:
Abel, N. H. "Oplösning af et Par Opgaver ved Hjelp af bestemt Integraler." Mag. for naturvidenskaberne 1, 55-68, 1823. Reprinted as "Solution de quelques problémes à l'aide d'intégrales définies." Paper II in Abel, N. H. Œ (Ed. L. Sylow and S. Lie). Christiania [Oslo], Norway, pp. 11-27, 1881. Reprinted by J. Gabay, 1992.
Abel, N. H. "Oplösning af nogle Opgaver ved Hjelp af bestemt Integraler." Mag. for naturvidenskaberne 1, 205-215, 1823. Reprinted as "Solution de quelques problémes à l'aide d'intégrales définies." Paper II in Abel, N. H. Œ (Ed. L. Sylow and S. Lie). Christiania [Oslo], Norway, 1881. Reprinted by J. Gabay, 1992.
Sloane, N. J. A. Sequence A102047 in "The On-Line Encyclopedia of Integer Sequences."
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
