المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | q-Pi |
 1359
 05:04 مساءً
date: 28-8-2019 |
Author : Sloane, N. J. A. 
Book or Source : Sequences A144874 and A144875 in "The On-Line Encyclopedia of Integer Sequences." 
Page and Part : ...|
Read More
Date: 21-5-2019
2044
Date: 1-8-2019
2898
Date: 12-9-2019
1946
|
The q-analog of pi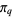 
can be defined by setting 
in the q-factorial
![[a]_q!=1(1+q)(1+q+q^2)...(1+q+...+q^(a-1))](http://mathworld.wolfram.com/images/equations/q-Pi/NumberedEquation1.gif) |
(1) |
to obtain
![1=sin_q^*(1/2pi)=(pi_q)/(([-1/2]_(q^2)!)^2q^(1/4)),](http://mathworld.wolfram.com/images/equations/q-Pi/NumberedEquation2.gif) |
(2) |
where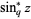 
is Gosper's q-sine, so
 |
 |
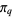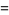![q^(1/4)([-1/2]_(q^2)!)^2](http://mathworld.wolfram.com/images/equations/q-Pi/Inline6.gif) |
(3) |
 |
 |
 |
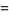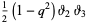(4) |
 |
 |
 |
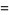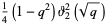(5) |
 |
 |
 |
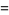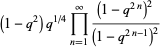(6) |
(Gosper 2001).
It has the Maclaurin series
 |
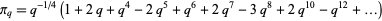(7) |
(OEIS A144874).
It is related to the q-analog of the Wallis formula (Gosper 2001), and has the special value
 |
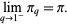(8) |
The area under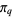 
is given by
 |
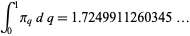(9) |
(OEIS A144875).
Gosper has developed an iterative algorithm for computing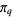 
based on the algebraic recurrence relation
 |
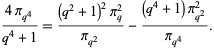(10) |
REFERENCES:
Sloane, N. J. A. Sequences A144874 and A144875 in "The On-Line Encyclopedia of Integer Sequences."
Gosper, R. W. "Experiments and Discoveries in q-Trigonometry." In Symbolic Computation, Number Theory,Special Functions, Physics and Combinatorics. Proceedings of the Conference Held at the University of Florida, Gainesville, FL, November 11-13, 1999 (Ed. F. G. Garvan and M. E. H. Ismail). Dordrecht, Netherlands: Kluwer, pp. 79-105, 2001.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
موكب خدمة الجوادين يقيم مجلساً عزائياً لإحياء ذكرى هدم مراقد أئمة البقيع "عليهم السلام"
|
|
|
