المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Bailey,s Theorem |
 1851
 04:37 مساءً
date: 21-5-2019 |
Author : Bailey, W. N. 
Book or Source : "The Partial Sum of the Coefficients of the Hypergeometric Series." J. London Math. Soc. 6, 
Page and Part : ...|
Read More
Date: 18-7-2019
1215
Date: 26-7-2019
1890
Date: 9-8-2019
1421
|
Let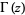 
be the gamma function and 
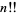denote a double factorial, then
![[(Gamma(m+1/2))/(Gamma(m))]^2[1/m+(1/2)^21/(m+1)+((1·3)/(2·4))^21/(m+2)+...]_()_(n)
=[(Gamma(n+1/2))/(Gamma(n))]^2[1/n+(1/2)^21/(n+1)+((1·3)/(2·4))^21/(n+2)+...]_()_(m).](http://mathworld.wolfram.com/images/equations/BaileysTheorem/NumberedEquation1.gif) |
Writing the sums explicitly, Bailey's theorem states
![[(Gamma(m+1/2))/(Gamma(m))]^2sum_(k=0)^(n-1)1/(m+k)[((2k-1)!!)/((2k)!!)]^2
=[(Gamma(n+1/2))/(Gamma(n))]^2sum_(k=0)^(m-1)1/(n+k)[((2k-1)!!)/((2k)!!)]^2.](http://mathworld.wolfram.com/images/equations/BaileysTheorem/NumberedEquation2.gif) |
REFERENCES:
Bailey, W. N. "The Partial Sum of the Coefficients of the Hypergeometric Series." J. London Math. Soc. 6, 40-41, 1931.
Bailey, W. N. "On One of Ramanujan's Theorems." J. London Math. Soc. 7, 34-36, 1932.
Darling, H. B. C. "On a Proof of One of Ramanujan's Theorems." J. London Math. Soc. 5, 8-9, 1930.
Hardy, G. H. Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work, 3rd ed. New York: Chelsea, pp. 106-107 and 112, 1999.
Hodgkinson, J. "Note on One of Ramanujan's Theorems." J. London Math. Soc. 6, 42-43, 1931.
Watson, G. N. "Theorems Stated by Ramanujan (VIII): Theorems on Divergent Series." J. London Math. Soc. 4, 82-86, 1929.
Watson, G. N. "The Constants of Landau and Lebesgue." Quart. J. Math. (Oxford) 1, 310-318, 1930.
Whipple, F. J. W. "The Sum of the Coefficients of a Hypergeometric Series." J. London Math. Soc. 5, 192, 1930.
|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|
