Inverse Tangent Integral

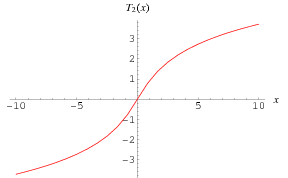
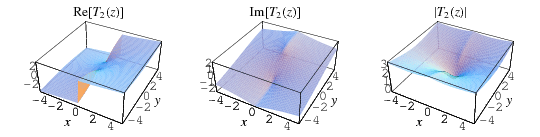
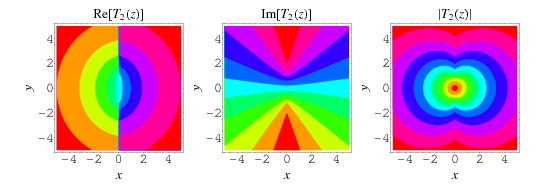
The inverse tangent integral 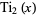 is defined in terms of the dilogarithm  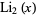by

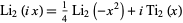(1)

(Lewin 1958, p. 33). It has the series

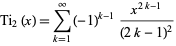(2)

and gives in closed form the sum

(3)

that was considered by Ramanujan (Lewin 1958, p. 39). The inverse tangent integral can be expressed in terms of the dilogarithm as

(4)

in terms of Legendre's chi-function as

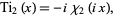(5)

in terms of the Lerch transcendent by

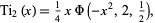(6)

and as the integral

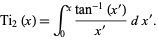(7)

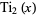 has derivative

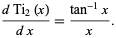(8)

It satisfies the identities

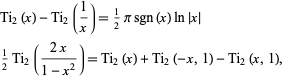(9)

where

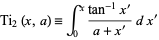(10)

is the generalized inverse tangent function.

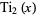 has the special value

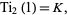(11)

where 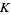 is Catalan's constant, and the functional relationships

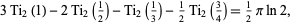(12)

the two equivalent identities

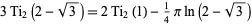(13)

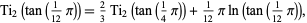(14)

and

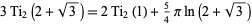(15)

(Lewin 1958, p. 39). The triplication formula is given by

(16)

which leads to

(17)

and the algebraic form

(18)

(Lewin 1958, p. 41).

REFERENCES:

Finch, S. R. "Inverse Tangent Integral." §1.7.6 in Mathematical Constants. Cambridge, England: Cambridge University Press, p. 57, 2003.

Lewin, L. "The Inverse Tangent Integral" and "The Generalized Inverse Tangent Integral." Chs. 2-3 in Dilogarithms and Associated Functions. London: Macdonald, pp. 33-90, 1958.

Lewin, L. Polylogarithms and Associated Functions. Amsterdam, Netherlands: North-Holland, p. 45, 1981.

Nielsen, N. "Der Eulersche Dilogarithmus und seine Verallgemeinerungen." Nova Acta Leopoldina, Abh.der Kaiserlich Leopoldinisch-Carolinischen Deutschen Akad. der Naturforsch. 90, 121-212, 1909.