Mellin-Barnes Integral

A type of integral containing gamma functions in its integrand. A typical such integral is given by

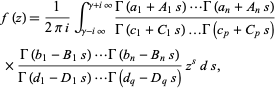where 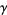 is real, 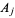, , 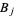, 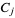and 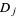 are positive, and the contour is a straight line parallel to the imaginary axis with indentations if necessary to avoid poles of the integrand.

REFERENCES:

Barnes, E. W. "A New Development in the Theory of the Hypergeometric Functions." Proc. London Math. Soc. 6, 141-177, 1908.

Dixon, A. L. and Ferrar, W. L. "A Class of Discontinuous Integrals." Quart. J. Math. (Oxford Ser.) 7, 81-96, 1936.

Erdélyi, A.; Magnus, W.; Oberhettinger, F.; and Tricomi, F. G. "Mellin-Barnes Integrals." §1.19 in Higher Transcendental Functions, Vol. 1. New York: Krieger, pp. 49-50, 1981.

Mellin, H. "Om Definita Integraler." Acta Societatis Scientiarum Fennicae 20, No. 7, 1-39, 1895.

Mellin, H. "Abrißeiner einheitlichen Theorie der Gamma- und der hypergeometrischen Funktionen." Math. Ann. 68, 305-337, 1909.

Paris, R. B. and Kaminski, D. Asymptotics and Mellin-Barnes Integrals. Cambridge, England: Cambridge University Press, 2001.

Pincherle, S. Atti d. R. Academia dei Lincei, Ser. 4, Rendiconti 4, 694-700 and 792-799, 1888.

Ramanujan, S. Collected Papers of Srinivasa Ramanujan (Ed. G. H. Hardy, P. V. S. Aiyar, and B. M. Wilson). Providence, RI: Amer. Math. Soc., p. 216, 2000.

Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England: Cambridge University Press, p. 289, 1990.