Arithmetic Mean

The arithmetic mean of a set of values is the quantity commonly called "the" mean or the average. Given a set of samples 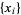, the arithmetic mean is

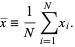(1)

It can be computed in the Wolfram Language using Mean[list].

The arithmetic mean is the special case 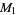 of the power mean and is one of the Pythagorean means.

When viewed as an estimator for the mean of the underlying distribution (known as the population mean), the arithmetic mean of a sample is called the sample mean.

For a continuous distribution function, the arithmetic mean of the population, denoted 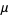, , , 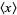or 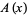 and called the population mean of the distribution, is given by

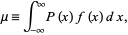(2)

where 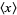 is the expectation value. Similarly, for a discrete distribution,

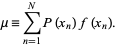(3)

The arithmetic mean satisfies

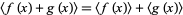(4)

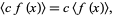(5)

and

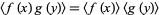(6)

if  and 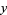 are independent statistics. The "sample mean," which is the mean estimated from a statistical sample, is an unbiased estimator for the population mean.

Hoehn and Niven (1985) show that

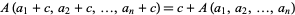(7)

for any constant 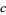. For positive arguments, the arithmetic mean satisfies

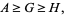(8)

where 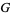 is the geometric mean and  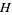is the harmonic mean (Hardy et al. 1952, Mitrinović 1970, Beckenbach and Bellman 1983, Bullen et al. 1988, Mitrinović et al. 1993, Alzer 1996). This can be shown as follows. For ,

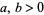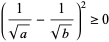(9)

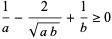(10)

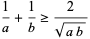(11)

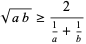(12)

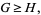(13)

with equality iff 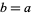. To show the second part of the inequality,

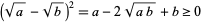(14)

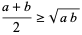(15)

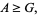(16)

with equality iff 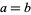. Combining (◇) and (◇) then gives (◇).

Given 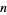 independent random normally distributed variates 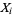, each with population mean  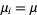and variance ,

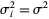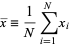(17)

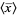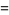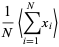			(18)
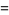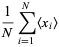			(19)
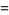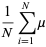			(20)
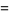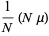			(21)
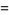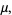			(22)

so the sample mean is an unbiased estimator of the population mean. However, the distribution of  depends on the sample size. For large samples,  is approximately normal. For small samples, Student's t-distribution should be used.

The variance of the sample mean is independent of the distribution, and is given by

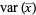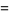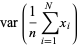			(23)
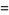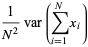			(24)
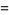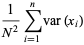			(25)
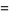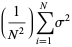			(26)
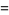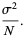			(27)

For small samples, the sample mean is a more efficient estimator of the population mean than the statistical median, and approximately 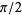 less (Kenney and Keeping 1962, p. 211). Here, an estimator of a parameter of a probability distribution is said to be more efficient than another one if it has a smaller variance. In this case, the variance of the sample mean is generally less than the variance of the sample median. The relative efficiency of two estimators is the ratio of this variance.

A general expression that often holds approximately is

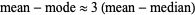(28)

(Kenney and Keeping 1962).

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 10, 1972.

Alzer, H. "A Proof of the Arithmetic Mean-Geometric Mean Inequality." Amer. Math. Monthly 103, 585, 1996.

Beckenbach, E. F. and Bellman, R. Inequalities. New York: Springer-Verlag, 1983.

Beyer, W. H. CRC Standard Mathematical Tables, 28th ed. Boca Raton, FL: CRC Press, p. 471, 1987.

Bullen, P. S.; Mitrinović, D. S.; and Vasić, P. M. Means and Their Inequalities. Dordrecht, Netherlands: Reidel, 1988.

Havil, J. Gamma: Exploring Euler's Constant. Princeton, NJ: Princeton University Press, pp. 119-121, 2003.

Hardy, G. H.; Littlewood, J. E.; and Pólya, G. Inequalities. Cambridge, England: Cambridge University Press, 1952.

Hoehn, L. and Niven, I. "Averages on the Move." Math. Mag. 58, 151-156, 1985.

Kenney, J. F. and Keeping, E. S. Mathematics of Statistics, Pt. 1, 3rd ed. Princeton, NJ: Van Nostrand, 1962.

Mitrinović, D. S. Analytic Inequalities. New York: Springer-Verlag, 1970.

Mitrinović, D. S.; Pečarić, J. E.; and Fink, A. M. Classical and New Inequalities in Analysis. Dordrecht, Netherlands: Kluwer, 1993.

Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 601, 1995.