المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Darling,s Products |
 1688
 05:59 مساءً
date: 15-6-2019 |
Author : Bailey, W. N. 
Book or Source : "Darling,s Theorems of Products." §10.3 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press 
Page and Part : pp. 88-92|
Read More
Date: 10-10-2019
1860
Date:
1619
Date: 9-10-2019
1744
|
A generalization of the hypergeometric function identity
 |
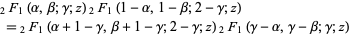(1) |
to the generalized hypergeometric function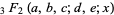 
. Darling's products are
![_3F_2[alpha,beta,gamma;z; delta,epsilon ]_3F_2[1-alpha,1-beta,1-gamma;z; 2-delta,2-epsilon ]
=(epsilon-1)/(epsilon-delta)_3F_2[alpha+1-delta,beta+1-delta,gamma+1-delta;z; 2-delta,epsilon+1-delta ]_3F_2[delta-alpha,delta-beta,delta-gamma;z; delta,delta+1-epsilon ]
+(delta-1)/(delta-epsilon)_3F_2[alpha+1-epsilon,beta+1-epsilon,gamma+1-epsilon;z; 2-epsilon,delta+1-epsilon ]_3F_2[epsilon-alpha,epsilon-beta,epsilon-gamma;z; epsilon,epsilon+1-delta ]](http://mathworld.wolfram.com/images/equations/DarlingsProducts/NumberedEquation2.gif) |
(2) |
and
![(1-z)^(alpha+beta+gamma-delta-epsilon)_3F_2[alpha,beta,gamma;z; delta,epsilon ]
=(epsilon-1)/(epsilon-delta)_3F_2[delta-alpha,delta-beta,delta-gamma;z; delta,delta+1-epsilon ]_3F_2[epsilon-alpha,epsilon-beta,epsilon-gamma;z; epsilon-1,epsilon+1-delta ]
+(delta-1)/(delta-epsilon)_3F_2[epsilon-alpha,epsilon-beta,epsilon-gamma;z; epsilon,epsilon+1-delta ]_3F_2[delta-alpha,delta-beta,delta-gamma;z; delta-1,delta+1-epsilon ],](http://mathworld.wolfram.com/images/equations/DarlingsProducts/NumberedEquation3.gif) |
(3) |
which reduce to (◇) when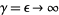 
.
REFERENCES:
Bailey, W. N. "Darling's Theorems of Products." §10.3 in Generalised Hypergeometric Series. Cambridge, England: Cambridge University Press, pp. 88-92, 1935.
|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|
