المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Euler,s Continued Fraction |
 1749
 01:39 صباحاً
date: 9-10-2019 |
Author : Borwein, J.; Bailey, D.; and Girgensohn, R. 
Book or Source : "Euler,s Continued Fraction." §1.8.2 in Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters 
Page and Part : p. 30|
Read More
Date: 22-5-2019
2800
Date: 9-10-2019
1917
Date: 23-8-2019
1176
|
Euler's continued fraction is the name given by Borwein et al. (2004, p. 30) to Euler's formula for the inverse tangent,
 |
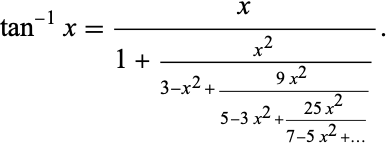An even more famous continued fraction related to Euler which is perhaps a more appropriate recipient of the appellation "Euler's continued fraction" is the simple continued fraction for e, namely
![e=[2;1,2,1,1,4,1,1,6,1,...].](http://mathworld.wolfram.com/images/equations/EulersContinuedFraction/NumberedEquation2.gif) |
REFERENCES:
Borwein, J.; Bailey, D.; and Girgensohn, R. "Euler's Continued Fraction." §1.8.2 in Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, p. 30, 2004.
|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|
