المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر
أضيف حديثاً
دين الله ولاية المهدي
2024-11-02
الميثاق على الانبياء الايمان والنصرة
2024-11-02
ما ادعى نبي قط الربوبية
2024-11-02
وقت العشاء
2024-11-02
نوافل شهر رمضان
2024-11-02
مواقيت الصلاة
2024-11-02

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
أحكام الخلل في الوضوء
6-12-2016
The Chemical Shift
7-8-2019
ما يستحب في الزوجة وما يكره
2024-02-04
ما المقصود بالمحاكاة الباتسيانية Batesian Mimics ؟
7-4-2021
الاحوال اجتماعية والحضارية في كندة
14-11-2016
فتح القسطنطينية (1261)
2023-11-09

Erfi  
  
1575   01:49 صباحاً   date: 28-4-2019
Author : Sloane, N. J. A.
Book or Source : Sequences A000079/M1129, A001147/M3002, and A084253 in "The On-Line Encyclopedia of Integer Sequences."
Page and Part : ...


Read More
Elementary Function
Date: 19-7-2019 3173
Riemann P-Series
Date: 18-6-2019 1303
Bailey,s Transformation
Date: 13-6-2019 1443

Erfi

 

ErfiReal
 
 
             
  Min Max      

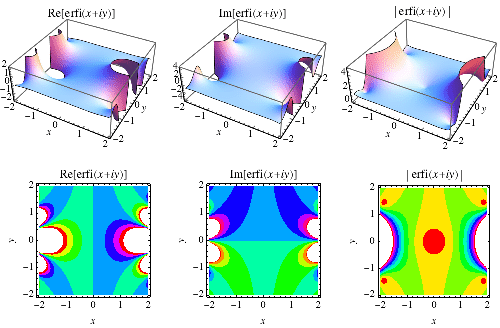ErfiReImAbs
 
 
  Min   Max    
  Re    
  Im      

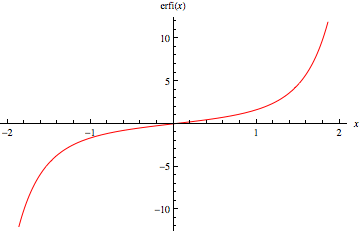
The "imaginary error function" 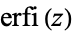erfi(z) is an entire function defined by

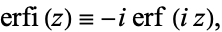erfi(z)=-ierf(iz),

(1)

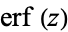where erf(z) is the erf function. It is implemented in the Wolfram Language as Erfi[z].

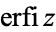erfiz has derivative

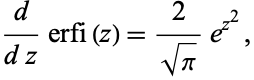d/(dz)erfi(z)=2/(sqrt(pi))e^(z^2),

(2)

and integral

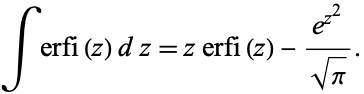interfi(z)dz=zerfi(z)-(e^(z^2))/(sqrt(pi)).

(3)

It has series about 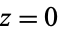z=0 given by

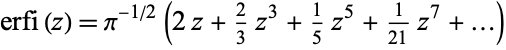erfi(z)=pi^(-1/2)(2z+2/3z^3+1/5z^5+1/(21)z^7+...)

(4)

(where the terms are OEIS A084253), and series about infinity given by

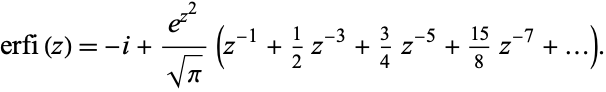erfi(z)=-i+(e^(z^2))/(sqrt(pi))(z^(-1)+1/2z^(-3)+3/4z^(-5)+(15)/8z^(-7)+...).

(5)

REFERENCES:

Sloane, N. J. A. Sequences A000079/M1129, A001147/M3002, and A084253 in "The On-Line Encyclopedia of Integer Sequences."




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
التاريخ / 2024-11-01

الأخبار العلمية
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
التاريخ / 2024-11-01

الساحة الاسلامية
المجمع العلميّ يُواصل عقد جلسات تعليميّة في فنون الإقراء لطلبة العلوم الدينيّة في النجف الأشرف
التاريخ / 2024-11-02