


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 15-6-2019
Date: 12-10-2018
Date: 24-3-2019
|
Bailey's transformation is the very general hypergeometric transformation
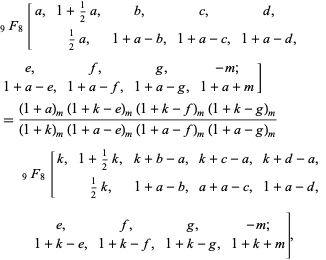 |
(1) |
where 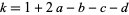 , and the parameters are subject to the restriction
, and the parameters are subject to the restriction
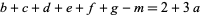 |
(2) |
(Bailey 1935, p. 27).
Bhatnagar (1995, pp. 17-18) defines a Bailey transform as follows. Let 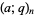 be the q-Pochhammer symbol, let
be the q-Pochhammer symbol, let 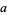 be an indeterminate, and let the lower triangular matrices
be an indeterminate, and let the lower triangular matrices 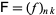 and
and 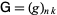 be defined as
be defined as
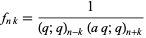 |
(3) |
and
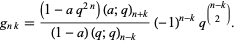 |
(4) |
Then 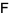 and
and 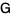 are matrix inverses.
are matrix inverses.
REFERENCES:
Bailey, W. N. "Some Identities Involving Generalized Hypergeometric Series." Proc. London Math. Soc. 29, 503-516, 1929.
Bailey, W. N. Generalised Hypergeometric Series. Cambridge, England: University Press, 1935.
Bhatnagar, G. Inverse Relations, Generalized Bibasic Series, and their U(n) Extensions. Ph.D. thesis. Ohio State University, 1995. http://www.math.ohio-state.edu/~milne/papers/Gaurav.whole.thesis.7.4.ps.
Milne, S. C. and Lilly, G. M. "The 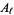 and
and 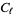 Bailey Transform and Lemma." Bull. Amer. Math. Soc. 26, 258-263, 1992.
Bailey Transform and Lemma." Bull. Amer. Math. Soc. 26, 258-263, 1992.



|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
|
|
|