المرجع الالكتروني للمعلوماتية
المرجع الألكتروني للمعلوماتية
ENGLISH
آخر المواضيع المضافة

الرياضيات
عدد المواضيع في هذا القسم 9761 موضوعاً
تاريخ الرياضيات
الرياضيات المتقطعة
الجبر
الضبابية
نظرية المجموعات
نظرية الزمر
نظرية الحلقات والحقول
نظرية الاعداد
نظرية الفئات
حساب المتجهات
المتتاليات-المتسلسلات
المصفوفات و نظريتها
المثلثات
الهندسة
التفاضل و التكامل
المعادلات التفاضلية و التكاملية
التحليل
التبلوجيا
نظرية الالعاب
الاحتمالات و الاحصاء
نظرية التحكم
بحوث العمليات
نظرية الكم
الشفرات
الرياضيات التطبيقية
نظريات ومبرهنات
علماء الرياضيات
الرياضيات في العلوم الاخرى
بحوث و اطاريح جامعية
هل تعلم
طرائق التدريس
الرياضيات العامة
نظرية البيان

Untitled Document
أبحث عن شيء أخر المرجع الالكتروني للمعلوماتية
أضيف حديثاً
تحليل فلسفي لمفهوم الشرور
2025-04-10
النواقص الحاصلة في المعلولين وتزاحم الأسباب
2025-04-10
إتكيت تعامل الإعلامي مع الشخصية الانطوائية أو الفُصامية
2025-04-09
إتكيت تعامل الإعلامي مع الشخصية المترددة
2025-04-09
إتكيت تعامل الإعلامي مع الشخص الثرثار
2025-04-09
إتكيت تعامل الإعلامي مع الشخصية النرجسية
2025-04-09

وثائقيات
العباءة العربية .. إرث الآباء واعتزاز الأبناء
التاريخ / 20-09-2024

مختارات
صياغة مشكلة البحث الإعلامي
2024-12-29
سم النحل Venom of Bee
12-8-2020
معنى كلمة هيج‌
2-1-2016
فوائد الزواج / التكميل والتكامل
2024-09-16
مفهوم الانتقال من الكُمُون الحراري إلى الحرارة الكامنة عند إبراهيم النَّظام (القرن 3هـ/9م)
2023-05-04
موضوع الكشف
16-3-2016

Weber,s Discontinuous Integrals  
  
1643   02:28 مساءً   date: 30-3-2019
Author : Bowman, F
Book or Source : Introduction to Bessel Functions. New York: Dover
Page and Part : pp. 59-60


Read More
Leibniz Series
Date: 13-10-2019 1539
Tanc Function
Date: 26-7-2019 1711
Inverse Erf
Date: 28-4-2019 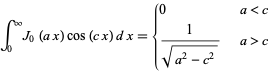1474

Weber's Discontinuous Integrals

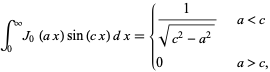int_0^inftyJ_0(ax)cos(cx)dx={0 a<c; 1/(sqrt(a^2-c^2)) a>c

(1)
int_0^inftyJ_0(ax)sin(cx)dx={1/(sqrt(c^2-a^2)) a<c; 0 a>c,

(2)

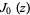where J_0(z) is a zeroth order Bessel function of the first kind.

REFERENCES:

Bowman, F. Introduction to Bessel Functions. New York: Dover, pp. 59-60, 1958.




الجبر أحد الفروع الرئيسية في الرياضيات، حيث إن التمكن من الرياضيات يعتمد على الفهم السليم للجبر. ويستخدم المهندسون والعلماء الجبر يومياً، وتعول المشاريع التجارية والصناعية على الجبر لحل الكثير من المعضلات التي تتعرض لها. ونظراً لأهمية الجبر في الحياة العصرية فإنه يدرّس في المدارس والجامعات في جميع أنحاء العالم. ويُعجب الكثير من الدارسين للجبر بقدرته وفائدته الكبيرتين، إذ باستخدام الجبر يمكن للمرء أن يحل كثيرًا من المسائل التي يتعذر حلها باستخدام الحساب فقط.وجاء اسمه من كتاب عالم الرياضيات والفلك والرحالة محمد بن موسى الخورازمي.


يعتبر علم المثلثات Trigonometry علماً عربياً ، فرياضيو العرب فضلوا علم المثلثات عن علم الفلك كأنهما علمين متداخلين ، ونظموه تنظيماً فيه لكثير من الدقة ، وقد كان اليونان يستعملون وتر CORDE ضعف القوسي قياس الزوايا ، فاستعاض رياضيو العرب عن الوتر بالجيب SINUS فأنت هذه الاستعاضة إلى تسهيل كثير من الاعمال الرياضية.

تعتبر المعادلات التفاضلية خير وسيلة لوصف معظم المـسائل الهندسـية والرياضـية والعلمية على حد سواء، إذ يتضح ذلك جليا في وصف عمليات انتقال الحرارة، جريان الموائـع، الحركة الموجية، الدوائر الإلكترونية فضلاً عن استخدامها في مسائل الهياكل الإنشائية والوصف الرياضي للتفاعلات الكيميائية.
ففي في الرياضيات, يطلق اسم المعادلات التفاضلية على المعادلات التي تحوي مشتقات و تفاضلات لبعض الدوال الرياضية و تظهر فيها بشكل متغيرات المعادلة . و يكون الهدف من حل هذه المعادلات هو إيجاد هذه الدوال الرياضية التي تحقق مشتقات هذه المعادلات.





الأخبار الصحية
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
التاريخ / 2025-04-08

الأخبار العلمية
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
التاريخ / 2025-04-08

الساحة الاسلامية
العتبة العباسية المقدسة تبحث مع العتبة الحسينية المقدسة التنسيق المشترك لإقامة حفل تخرج طلبة الجامعات
التاريخ / 2025-04-09