


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-8-2019
Date: 13-10-2019
Date: 9-8-2019
|
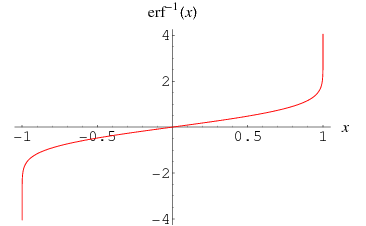
The inverse erf function is the inverse function 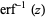 of the erf function
of the erf function 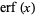 such that
such that
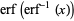 |
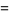 |
 |
(1) |
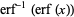 |
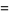 |
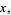 |
(2) |
with the first identity holding for 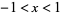 and the second for
and the second for 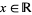 . It is implemented in the Wolfram Language as InverseErf[x].
. It is implemented in the Wolfram Language as InverseErf[x].
It is an odd function since
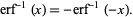 |
(3) |
It has the special values
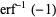 |
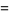 |
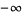 |
(4) |
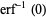 |
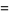 |
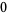 |
(5) |
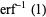 |
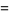 |
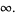 |
(6) |
It is apparently not known if
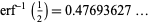 |
(7) |
(OEIS A069286) can be written in closed form.
It satisfies the equation
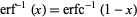 |
(8) |
where 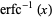 is the inverse erfc function.
is the inverse erfc function.
It has the derivative
![d/(dx)erf^(-1)(x)=1/2sqrt(pi)e^([erf^(-1)(x)]^2),](http://mathworld.wolfram.com/images/equations/InverseErf/NumberedEquation4.gif) |
(9) |
and its integral is
![interf^(-1)(x)dx=-(e^(-[erf^(-1)(x)]^2))/(sqrt(pi))](http://mathworld.wolfram.com/images/equations/InverseErf/NumberedEquation5.gif) |
(10) |
(which follows from the method of Parker 1955).
Definite integrals are given by
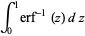 |
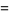 |
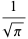 |
(11) |
 |
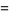 |
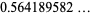 |
(12) |
![int_0^1ln[erf^(-1)(z)]dz](http://mathworld.wolfram.com/images/equations/InverseErf/Inline27.gif) |
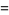 |
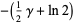 |
(13) |
 |
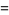 |
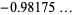 |
(14) |
(OEIS A087197 and A114864), where 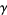 is the Euler-Mascheroni constant and
is the Euler-Mascheroni constant and 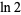 is the natural logarithm of 2.
is the natural logarithm of 2.
The Maclaurin series of 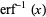 is given by
is given by
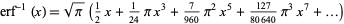 |
(15) |
(OEIS A002067 and A007019). Written in simplified form so that the coefficient of  is 1,
is 1,
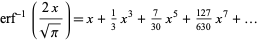 |
(16) |
(OEIS A092676 and A092677). The 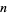 th coefficient of this series can be computed as
th coefficient of this series can be computed as
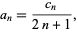 |
(17) |
where 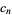 is given by the recurrence equation
is given by the recurrence equation
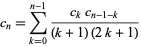 |
(18) |
with initial condition 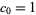 .
.
REFERENCES:
Bergeron, F.; Labelle, G.; and Leroux, P. Ch. 5 in Combinatorial Species and Tree-Like Structures. Cambridge, England: Cambridge University Press, 1998.
Carlitz, L. "The Inverse of the Error Function." Pacific J. Math. 13, 459-470, 1963.
Parker, F. D. "Integrals of Inverse Functions." Amer. Math. Monthly 62, 439-440, 1955.
Sloane, N. J. A. Sequences A002067/M4458, A007019/M3126, A069286, A087197, A092676, A092677, A114859, A114860, and A114864 in "The On-Line Encyclopedia of Integer Sequences."



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|