Principle of Permanence

In its simplest form, the principle of permanence states that, given any analytic function 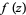 defined on an open (and connected) set  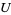of the complex numbers 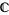, and a convergent sequence  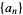which along with its limit  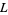belongs to 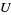, such that  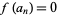for all 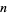, then  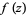is uniformly zero on .

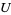This is easily proved by showing that the Taylor series of 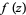 about 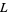 must have all its coefficients equal to 0.

The principle of permanence has wide-ranging consequences. For example, if 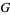 and 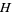 are analytic functions defined on 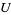, then any functional equation of the form

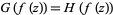that is true for all 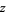 in a closed subset of  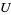having a limit point in  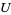(e.g., a nonempty open subset of 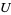) must be true for all  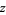in .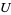

REFERENCES:

Wolfram, S. A New Kind of Science. Champaign, IL: Wolfram Media, p. 1168, 2002.