


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 11-6-2018
Date: 20-8-2018
|
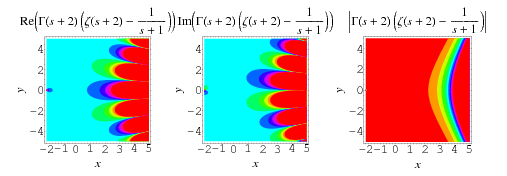

Hadjicostas's formula is a generalization of the unit square double integral
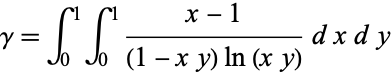 |
(1) |
(Sondow 2003, 2005; Borwein et al. 2004, p. 49), where  is the Euler-Mascheroni constant. It states
is the Euler-Mascheroni constant. It states
![int_0^1int_0^1(1-x)/(1-xy)[-ln(xy)]^sdxdy
=Gamma(s+2)[zeta(s+2)-1/(s+1)]](http://mathworld.wolfram.com/images/equations/HadjicostassFormula/NumberedEquation2.gif) |
(2) |
for ![Re[s]>-2](http://mathworld.wolfram.com/images/equations/HadjicostassFormula/Inline2.gif) , where
, where  is the gamma function and
is the gamma function and 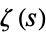 is the Riemann zeta function (although care must be taken at
is the Riemann zeta function (although care must be taken at 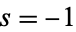 because of the removable singularity present there). It was conjectured by Hadjicostas (2004) and almost immediately proved by Chapman (2004). The special case
because of the removable singularity present there). It was conjectured by Hadjicostas (2004) and almost immediately proved by Chapman (2004). The special case 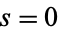 gives Beukers's integral for
gives Beukers's integral for 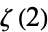 ,
,
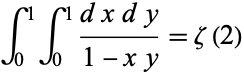 |
(3) |
(Beukers 1979). At 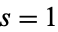 , the formula is related to Beukers's integral for Apéry's constant
, the formula is related to Beukers's integral for Apéry's constant 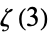 , which is how interest in this class of integrals originally arose.
, which is how interest in this class of integrals originally arose.
There is an analogous formula
![int_0^1int_0^1(1-x)/(1+xy)[-ln(xy)]^sdxdy
=Gamma(s+2)[eta(s+2)+(1-2eta(s+1))/(s+1)]](http://mathworld.wolfram.com/images/equations/HadjicostassFormula/NumberedEquation4.gif) |
(4) |
for ![R[s]>-3](http://mathworld.wolfram.com/images/equations/HadjicostassFormula/Inline10.gif) , due to Sondow (2005), where
, due to Sondow (2005), where 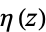 is the Dirichlet eta function. This includes the special cases
is the Dirichlet eta function. This includes the special cases
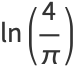 |
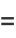 |
![sum_(n=1)^(infty)(-1)^(n-1)[1/n-ln((n+1)/n)]](http://mathworld.wolfram.com/images/equations/HadjicostassFormula/Inline14.gif) |
(5) |
 |
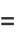 |
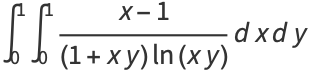 |
(6) |
 |
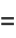 |
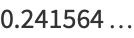 |
(7) |
(OEIS A094640; Sondow 2005) and
![int_0^1int_0^1(1-x)/((1+xy)[ln(xy)]^2)dxdy](http://mathworld.wolfram.com/images/equations/HadjicostassFormula/Inline21.gif) |
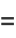 |
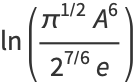 |
(8) |
 |
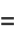 |
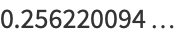 |
(9) |
REFERENCES:
Beukers, F. "A Note on the Irrationality of 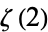 and
and 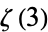 ." Bull. London Math. Soc. 11, 268-272, 1979.
." Bull. London Math. Soc. 11, 268-272, 1979.
Borwein, J.; Bailey, D.; and Girgensohn, R. Experimentation in Mathematics: Computational Paths to Discovery. Wellesley, MA: A K Peters, 2004.
Chapman, R. "A Proof of Hadjicostas's Conjecture." 15 Jun 2004. http://arxiv.org/abs/math/0405478.
Guillera, J. and Sondow, J. "Double Integrals and Infinite Products for Some Classical Constants Via Analytic Continuations of Lerch's Transcendent." 16 June 2005 http://arxiv.org/abs/math.NT/0506319.
Hadjicostas, P. "A Conjecture-Generalization of Sondow's Formula." 21 May 2004. http://www.arxiv.org/abs/math.NT/0405423/.
Sloane, N. J. A. Sequences A094640, A103130 in "The On-Line Encyclopedia of Integer Sequences."
Sondow, J. "Criteria for Irrationality of Euler's Constant." Proc. Amer. Math. Soc. 131, 3335-3344, 2003. http://arxiv.org/abs/math.NT/0209070.
Sondow, J. "Double Integrals for Euler's Constant and 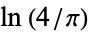 and an Analog of Hadjicostas's Formula." Amer. Math. Monthly112, 61-65, 2005.
and an Analog of Hadjicostas's Formula." Amer. Math. Monthly112, 61-65, 2005.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|