


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 21-7-2018
Date: 23-7-2018
Date: 21-7-2018
|
In conical coordinates, Laplace's equation can be written
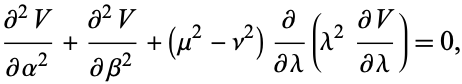 |
(1)
|
where
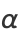 |
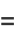 |
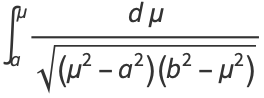 |
(2)
|
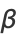 |
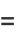 |
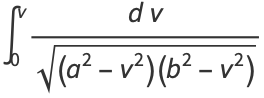 |
(3)
|
(Byerly 1959). Letting
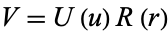 |
(4)
|
breaks (1) into the two equations,
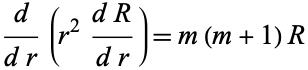 |
(5)
|
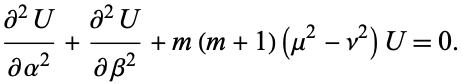 |
(6)
|
Solving these gives
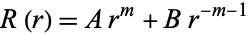 |
(7)
|
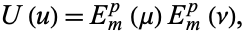 |
(8)
|
where 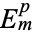 are ellipsoidal harmonics of the first kind. The regular solution is therefore
are ellipsoidal harmonics of the first kind. The regular solution is therefore
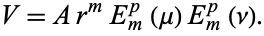 |
(9)
|
However, because of the cylindrical symmetry, the solution 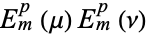 is an
is an 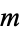 th degree spherical harmonic.
th degree spherical harmonic.
REFERENCES:
Arfken, G. "Conical Coordinates 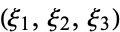 ." §2.16 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 118-119, 1970.
." §2.16 in Mathematical Methods for Physicists, 2nd ed. Orlando, FL: Academic Press, pp. 118-119, 1970.
Byerly, W. E. An Elementary Treatise on Fourier's Series, and Spherical, Cylindrical, and Ellipsoidal Harmonics, with Applications to Problems in Mathematical Physics. New York: Dover, p. 263, 1959.
Moon, P. and Spencer, D. E. Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions, 2nd ed. New York: Springer-Verlag, pp. 39-40, 1988.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, pp. 514 and 659, 1953.



|
|
|
|
مخاطر خفية لمكون شائع في مشروبات الطاقة والمكملات الغذائية
|
|
|
|
|
|
|
"آبل" تشغّل نظامها الجديد للذكاء الاصطناعي على أجهزتها
|
|
|
|
|
|
|
تستخدم لأول مرة... مستشفى الإمام زين العابدين (ع) التابع للعتبة الحسينية يعتمد تقنيات حديثة في تثبيت الكسور المعقدة
|
|
|