Singular Point

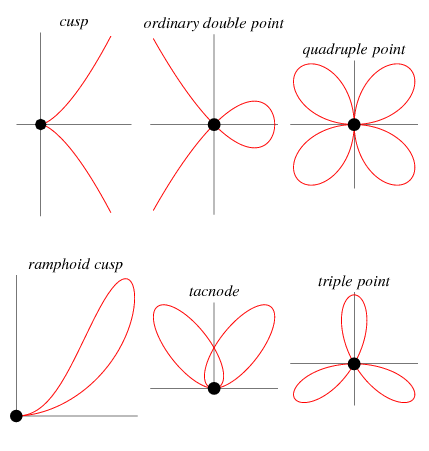
A singular point of an algebraic curve is a point where the curve has "nasty" behavior such as a cusp or a point of self-intersection (when the underlying field 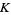 is taken as the reals). More formally, a point  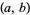on a curve  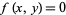is singular if the  and 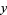 partial derivatives of  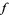are both zero at the point 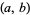. (If the field  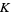is not the reals or complex numbers, then the partial derivative is computed formally using the usual rules of calculus.)

The following table gives some representative named curves that have various types of singular points at their origin.

singularity	curve	equation
acnode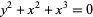
cusp	cusp curve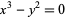
crunode	cardioid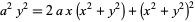
quadruple point	quadrifolium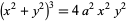
ramphoid cusp	keratoid cusp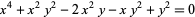
tacnode	capricornoid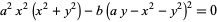
triple point	trifolium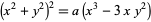

Consider the following two examples. For the curve

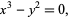the cusp at (0, 0) is a singular point. For the curve

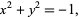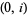 is a nonsingular point and this curve is nonsingular.

Singular points are sometimes known as singularities, and vice versa.

REFERENCES:

Arfken, G. "Singularities" and "Singular Points." §7.1 and 8.4 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 396-400 and 451-454, 1985.