


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 27-5-2018
Date: 12-6-2018
Date: 5-7-2018
|
Any locally compact Hausdorff topological group has a unique (up to scalars) nonzero left invariant measure which is finite on compact sets. If the group is Abelian or compact, then this measure is also right invariant and is known as the Haar measure.
More formally, let 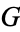 be a locally compact group. Then a left invariant Haar measure on
be a locally compact group. Then a left invariant Haar measure on 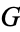 is a Borel measure
is a Borel measure 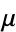 satisfying the following conditions:
satisfying the following conditions:
1. 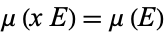 for every
for every 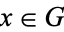 and every measurable
and every measurable 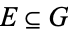 .
.
2. 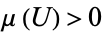 for every nonempty open set
for every nonempty open set 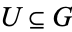 .
.
3. 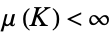 for every compact set
for every compact set 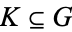 .
.
For example, the Lebesgue measure is an invariant Haar measure on real numbers.
In addition, if 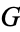 is an (algebraic) group, then
is an (algebraic) group, then 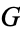 with the discrete topology is a locally compact group. A left invariant Haar measure on
with the discrete topology is a locally compact group. A left invariant Haar measure on 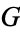 is the counting measure on
is the counting measure on 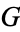 .
.
REFERENCES:
Conway, J. A Course in Functional Analysis. New York: Springer-Verlag, 1990.
Feldman M. and Gilles, C. "An Expository Note on Individual Risk Without Aggregate Uncertainty." J. Econ. Theory 35, 26-32, 1985.



|
|
|
|
"إنقاص الوزن".. مشروب تقليدي قد يتفوق على حقن "أوزيمبيك"
|
|
|
|
|
|
|
الصين تحقق اختراقا بطائرة مسيرة مزودة بالذكاء الاصطناعي
|
|
|
|
|
|
|
قسم شؤون المعارف ووفد من جامعة البصرة يبحثان سبل تعزيز التعاون المشترك
|
|
|