المرجع الألكتروني للمعلوماتية
القرآن الكريم وعلومه
العقائد الإسلامية
الفقه وأصوله 
الرجال والحديث 
سيرة الرسول وآله 
علوم اللغة العربية 
الأدب العربي 
الأسرة والمجتمع 
الأخلاق والأدعية 
التاريخ 
الادارة والاقتصاد 
علم الفيزياء 
علم الكيمياء 
علم الأحياء 
الرياضيات 
الهندسة المدنية 
الزراعة 
الجغرافية 
القانون 
اللغة الأنكليزية 
الأخبار 
الإعلام 
مكتبة الصور 
أقلام بمختلف الألوان 
إضاءات
مفتاح
أجوبة الإستفتاءات الشرعية
وثائقيات
تاريخ الرياضيات
الرياضيات في الحضارات المختلفة
الرياضيات المتقطعة
الجبر
الهندسة
المعادلات التفاضلية و التكاملية
التحليل
علماء الرياضيات | Heaviside Calculus |
 789
 03:10 مساءً
date: 12-6-2018 |
Author : Rota, G.-C.; Kahaner, D.; Odlyzko, A 
Book or Source : "On the Foundations of Combinatorial Theory. VIII: Finite Operator Calculus." J. Math. Anal. Appl 
Page and Part : ...|
Read More
Date: 22-6-2018
1811
Date: 27-5-2018
1016
Date: 5-7-2018
1475
|
The study, first developed by Boole, of shift-invariant operators which are polynomials in the differential operator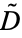 
. Heaviside calculus can be used to solve any ordinary differential equation of the form
 |
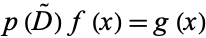with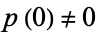 
, and is frequently implemented using Laplace transforms.
REFERENCES:
Rota, G.-C.; Kahaner, D.; Odlyzko, A. "On the Foundations of Combinatorial Theory. VIII: Finite Operator Calculus." J. Math. Anal. Appl. 42, 684-760, 1973.
|
|
|
|
4 أسباب تجعلك تضيف الزنجبيل إلى طعامك.. تعرف عليها
|
|
|
|
|
|
|
أكبر محطة للطاقة الكهرومائية في بريطانيا تستعد للانطلاق
|
|
|
|
|
|
|
أصواتٌ قرآنية واعدة .. أكثر من 80 برعماً يشارك في المحفل القرآني الرمضاني بالصحن الحيدري الشريف
|
|
|
