


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات |
Read More
Date: 24-3-2019
Date: 12-8-2018
Date: 23-9-2019
|
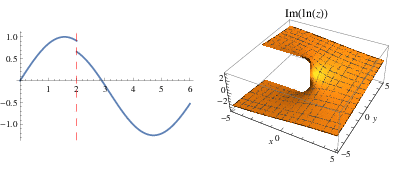
A discontinuity is point at which a mathematical object is discontinuous. The left figure above illustrates a discontinuity in a one-variable function while the right figure illustrates a discontinuity of a two-variable function plotted as a surface in 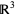 . In the latter case, the discontinuity is a branch cut along the negative real axis of the natural logarithm
. In the latter case, the discontinuity is a branch cut along the negative real axis of the natural logarithm 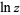 for complex
for complex 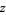 .
.
Some authors refer to a discontinuity of a function as a jump, though this is rarely utilized in the literature.
Though defined identically, discontinuities of univariate functions are considerably different than those of multivariate functions. One of the main differences between these cases exists with regards to classifying the discontinuities, a caveat discussed more at length below.
In the case of a one-variable real-valued function 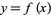 , there are precisely three families of discontinuities that can occur.
, there are precisely three families of discontinuities that can occur.
1. The simplest type is the so-called removable discontinuity.
2. A univariate function 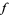 may also have what's known as a jump discontinuity (not to be confused with the rarely-utilized term jump mentioned above). This discontinuity is algebraically less-trivial than a removable discontinuity but is, in some sense, still a "not terrible" discontinuity. In particular, univariate monotone functions can have at most countably many discontinuities (Royden and Fitzpatrick 2010), the worst of which can be jump discontinuities (Zakon 2004).
may also have what's known as a jump discontinuity (not to be confused with the rarely-utilized term jump mentioned above). This discontinuity is algebraically less-trivial than a removable discontinuity but is, in some sense, still a "not terrible" discontinuity. In particular, univariate monotone functions can have at most countably many discontinuities (Royden and Fitzpatrick 2010), the worst of which can be jump discontinuities (Zakon 2004).
3. The "worst" kind of discontinuity a univariate function can possess is the so-called infinite discontinuity.
Even with this classification, the sets of discontinuity of univariate real-valued functions may be stranger than unexpected. Indeed, functions may be discontinuous at finite sets of points, at countable sets of points which may be either isolated or dense, and on uncountable proper subsets of their domain. Other functions, such as the Dirichlet function, are discontinuous everywhere. Even so, the size of the discontinuity set of a function can say a lot about its analytic properties. For example, a theorem of Lebesgue states that a bounded univariate real-valued function defined on a bounded interval is Riemann integrable if and only if it is continuous almost everywhere (Royden and Fitzpatrick 2010); similarly, the sets of discontinuities of univariate monotone real-valued functions defined on open intervals are at most countable subsets of their domain.
With functions of two or more variables, however, no simple discontinuity classification is possible. There are a number of caveats which hinder any classification of the discontinuities of multivariate functions, chief among which is the fact that multivariate functions need neither jump nor "blow up" at points of discontinuity (Lady 1998). What's more, discontinuities of several-variable functions may occur along entire curves in the plane rather than at individual points. Various examples of discontinuous behavior are shown below.
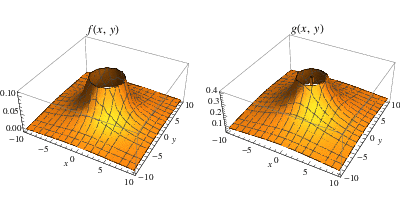
The two functions above both have infinite discontinuities at the origin. The leftmost example is the function 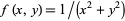 , which has the property that each of the directional limits of
, which has the property that each of the directional limits of 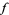 tends to
tends to 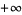 as
as 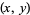 approaches
approaches 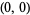 . On the other hand, the rightmost function is
. On the other hand, the rightmost function is
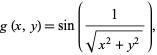 |
(1)
|
a function which has also a discontinuity as 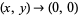 and for which
and for which 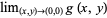 fails to exist. The function
fails to exist. The function 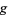 represents the surface obtained by revolving the function
represents the surface obtained by revolving the function 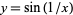 about the
about the  -axis.
-axis.
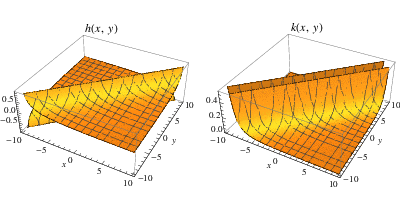
The two functions shown in the above figure are in some ways similar to the functions  and
and 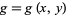 described above. More precisely, the function
described above. More precisely, the function 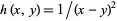 on the left has infinite discontinuity along the entire line
on the left has infinite discontinuity along the entire line 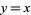 and the limit of
and the limit of 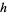 approaches
approaches 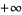 from both sides of that line. On the other hand, the function
from both sides of that line. On the other hand, the function  on the right has infinite discontinuity along the same line, but the limits of the values of
on the right has infinite discontinuity along the same line, but the limits of the values of  disagree on either side of that line.
disagree on either side of that line.
The function shown above is the piecewise function
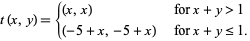 |
(2)
|
In particular, note that 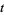 is monotone in each of
is monotone in each of  and
and 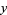 separately and has jump discontinuity along the entire line
separately and has jump discontinuity along the entire line 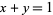 . This is in stark contrast to the univariate case, as discussed above.
. This is in stark contrast to the univariate case, as discussed above.
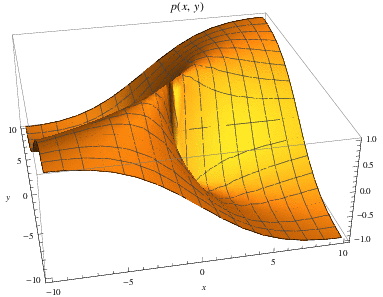
The function 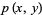 defined by
defined by
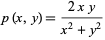 |
(3)
|
is shown in the figure immediately above. Like the functions 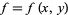 and
and 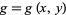 defined previously, the function
defined previously, the function 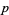 has a discontinuity at the point
has a discontinuity at the point 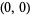 , though unlike those functions, the point discontinuity of
, though unlike those functions, the point discontinuity of 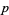 is more difficult to recognize. One way to observe and understand the discontinuity of
is more difficult to recognize. One way to observe and understand the discontinuity of 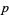 is by converting
is by converting 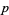 to a function of the polar coordinates
to a function of the polar coordinates 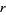 and
and 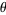 , the result of which is the function
, the result of which is the function 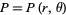 having the form
having the form
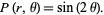 |
(4)
|
Among other things, the expression in (3) above shows that 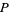 (and hence
(and hence 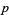 ) is constant on all lines through the origin (Lady 1998), thereby confirming the existence of a discontinuity there. This example is also unlike the cases outlined for univariate functions due to the fact that its discontinuity is essential (i.e., it is not removable) and is neither a jump nor an infinite discontinuity.
) is constant on all lines through the origin (Lady 1998), thereby confirming the existence of a discontinuity there. This example is also unlike the cases outlined for univariate functions due to the fact that its discontinuity is essential (i.e., it is not removable) and is neither a jump nor an infinite discontinuity.
Despite behaving very differently in terms of continuity, the sets of discontinuities of all real-valued functions in any dimension share certain properties. For example, the collection of discontinuities of such a function is always an 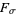 set; this is due to the fact that the set of all points at which a function is continuous form a
set; this is due to the fact that the set of all points at which a function is continuous form a 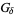 set (Royden and Fitzpatrick 2010).
set (Royden and Fitzpatrick 2010).
REFERENCES:
Gürsoy, A. B. "Functions of Several Variables and Partial Differentiation." 2013. http://mcs156.cankaya.edu.tr/uploads/files/Functions%20of%20Several%20Variables%20and%20Partial%20Differentiation.pdf.
Johnson, D. "A Sketch of the Theory of Functions of Several Variables."http://thewaythetruthandthelife.net/index/2_background/2-1_cosmological/math/mat6/calcul10.htm.
Lady, E. L. "Discontinuities for Functions of One and Two Variables." 1998. http://www.math.hawaii.edu/~lee/calculus/Discontinuous.pdf.
Royden, H. L. and Fitzpatrick, P. M. Real Analysis. Pearson, 2010.
Zakon, E. Mathematical Analysis Volume 1. West Lafayette, IN: The Trilla Group, 2004. http://www.trillia.com/zakon-analysisI.html.



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|