العمليات العشوائية

عندما تتحرك كل جسيمات البلازما وفق نظام منضبط مثل سير الجنود في استعراض رسمي. مثل هذه اللوحة تكون الحركة في البلازما الباردة. ولكن الحركة الحرارية تخرب مثل هذه اللوحة المنتظمة. بينما في البلازما الحارة تتحرك الجسيمات بشكل عشوائي كتلاميذ المدرسة في وقت الفرصة، والحركة الحرارية عشوائية. وهي تخضع فقط لقوانين الصدفة، التي تعبر عنها بلغة الرياضيات بواسطة نظرية الاحتمالات.

من المهم ان نشير هنا الى ان الحقل المغنطيسي ينظم حركة الجسيمات​ ويخضعها لنظام صارم. يأخذ مفهوم البلازما الباردة بوجود حقل مغنطيسي معني حقيقيا ومحددا على نحو كامل. وتدعى البلازما الباردة، التي يكون لديها ضغط الغاز p= nT  اصغر بالمقارنة مع الضغط المغنطيسي π pm = H2 / 8 وان النسبة بين هذين الضغطين تشكل مميزة هامة في البلازما الا وهي:

 β = p/ pm = nT 8π/ H² 

فعند قيمة صغيرة لـ β يمكن اعتبار البلازما باردة أي ان الحركة الحرارية في مثل هذه البلازما صغيرة الى حد الاهمال.

من المفيد مقارنة تعريفي البلازما الباردة والبلازما المتمغنطة. فالبلازما المتمغنطة تدعى تلك البلازما التي يكون لديها نصف القطر السيكلتروني صغيرا بالمقارنة مع ابعاد الجملة أي:

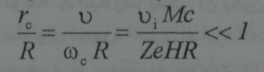
وهنا يؤخذ نصف القطر السيكلتروني الاكبر وبالتحديد نصف القطر السيكلتروني للايونات وبتربيع شرط التمغنط يكتب على الشكل:

حيث R نصف قطر حجم البلازما الذي يؤخذ على شكل اسطواني، ممطوط وفق طول الحقل ² _i M v ≈_┴i T درجة الحرارة الموافقة للحركة العرضية للايونات.

بضرب البسط والمقام بتركيز الايونات _i n يمكن تحويل شرط التمغنط الى الشكل :

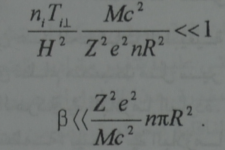
يقع في الطرف الايمن من هذه اللامساواة مقدار يدعى بالعدد الخطي للايونات . وهو العدد الكلي للايونات على طول الاسطوانة الذي يساوي طولها الى نصف القطر الكلاسيكي للايون Z² e² / Mc² اذا كان العدد الخطي للايونات كبيرا فان البلازما الباردة ستكون على الاغلب متمغنطة.

تظهر التجليات في الهامة للحركة الحرارية في عمليات: نقل المادة والحرارة وكمية الحركة (الاندفاع). يعبر عن نقل المادة بالحركة الحرارية بالانتثار، وعن نقل الحرارة بالناقلية الحرارية وعن كمية الحركة باللزوجة. وهناك في البلازما عملية نقل الشحنة أي التيار الكهربائي المتعلقة بالحركة الحرارية ايضا بحيث انه يمكن اضافة ناقلية البلازما الى عدد معاملات النقل فيها. ولكنها ليست ذات معنى بسيط كمعاملات الانتثار والناقلية الحرارية واللزوجة.

القانون الاساسي لكل العمليات العشوائية هذه هو قانون التبدد. لنأخذ مقدارا عشوائيا مميزا ليكن على سبيل المثال موضع الجسيمة او سرعتها التي تقوم بحركة حرارية عشوائية.

لنرمز لهذا المقدار بـ ƒ الذي يمكن ان يتغير بشكل عشوائي. نفترض اولا وللتبسيط ان المقدار ƒ يتغير على شكل قفزات، ويتغير عند كل قفزة بمقدار Δƒ مع العلم ان Δƒ وباحتمال متساو، ويمكن ان يكون موجبا ويمكن ان يكون سالبا.

عندئذ يكون مجموع كل هذه التغيرات:

بحيث ان القيمة الوسطية ƒ لا تتغير. ولكن مربعات هذه التغيرات موجبة بحيث ان مجوع المربعات:

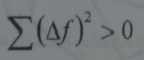
يتزايد مع الزمن هذا المجموع يدعى بالتبدد. ويخدم معيارا للفاصل الذي يكون ضمنه المقدار ƒ متأرجحا حول قيمة وسطية ثابتة. وكون ان التبدد يتصاعد متناسبا مع الزمن فانه يمكن كتابته على النحو التالي:

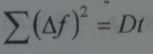
ويدعى ثابت التناسب D بمعامل الانتثار (النفوذية).

يمكن تعميم قانون التبدد على حالة يكون فيها المقدار ƒ معينا ليس فقط بالقيمة بل بالاتجاه ايضا أي هو مقدار متجه (شعاع) . عندها يؤول قانون التبدد الى قانون التجوالات العشوائية. يؤدي​ تجوال الجسيمات في الفراغ الاعتيادي الى عمليات النقل ويؤدي في فراغ السرع الى تبادل الطاقة بين درجات الحرية المختلفة وقيام التوازن الحراري.

مواضيع ذات صلة

الانتثار ثنائي القطبية

عمليات النقل في الحقل المغناطيسي

احلال التوازن الحراري

التصادمات الكولونية

التصادمات مع الجسيمات المعتدلة

مسار ومقطع التصادمات

امواج الصدم في البلازما

تخامد وحث الاهتزازات

المجاوبات البلازمية والدلائل الموجية

مرور الامواج العامة الراديوية عبر البلازما

الامواج المائلة والتصنيف العام للاهتزازات

التبدد بجوار التواترات السيكلترونية