اهتزازات البلازما في حقل مغناطيسي

يمكن ان تنشأ انواع عديدة من الاهتزازات في البلازما الواقعة في حقل مغناطيسي وابسط هذه الاهتزازات هي الاهتزازات التي تنتشر موازية او معامدة للحقل المغناطيسي . وفي هاتين الحالتين البسيطتين من الاهتزازات يتولد نوعان من الاهتزازات المستقلة يكون فيهما الحقل الكهربائي متجها وفق اتجاه الحقل المغناطيسي. فمن اجل الانتشار الموازي للحقل المغناطيسي تكون الاهتزازات البلازمية الكهروساكنة طولية. ومن اجل الانتشار المتعامد على الحقل المغناطيسي تكون الموجة الكهرطيسية عرضية ولما كان الحقل المغناطيسي لا يؤثر على التيار المتجه وفقه، لذلك فالحقل لن يؤثر على هذه الانواع من الاهتزازات⁽¹⁾.

من هنا تنشأ امكانية سبر او حبس البلازما بموجة كهرطيسية منتشرة بشكل عرضي على الحقل المغنطيسي ولكنها مستقطبة وفق اتجاه الحقل.

تستخدم هذه الطريقة في السبر على نحو واسع في تشخيص البلازما . مثل هذه الموجة تنفذ في البلازما فقط اذا تحقق شرط ان يكون تواتر الموجة اعلى من تواتر البلازما (كما في حالة غياب حقل مغناطيسي).

اذا كان اتجاه انتشار الموجة موازيا او معامدا للحقل المغنطيسي فانه يمكن نشر اي موجة مهما كان اتجاه حقلها الكهربائي الموازي لحقل المغنطيسي. والثانية على وجه التحديد ذات الحقل الكهربائي المعامد للحقل المغنطيسي التي تعد مصدر انواع جديدة من الاهتزازات المميزة للبلازما الواقعة في حقل مغنطيسي .

اذا كان تواتر الموجه صغير بالمقترنة مع الموجة السيكلترونية (وبالتحديد مع اصغرها الا وهو التواتر الايوني) فان البلازما تسلك ببساطة سلوك سائل ناقل الذي يوصف بمعادلات الهدروديناميك المغنطيسي. في هذا المجال من التواترات تنتشر امواج الففين Alfeen او امواج الهيدروديناميك المغنطيسي وفق اتجاه موازي للحقل المغنطيسي وفي الاتجاه المتعامد مع الحقل تنتشر الامواج الصوتية المغنطيسية .

يمكن تصور الطبيعة الفيزيائية لهذه الانواع من الاهتزازات بوضوح باستخدام مفهوم الحقل المغنطيسي المتجمد. وفي حالتي الانتشار تتحرك خطوط القوة المغنطيسية في آن معا مع المادة وتنتقل هذه المادة في الموجة الصوتية – المغنطيسية على طول منحى الانتشار وتشبه الية انتشار هذه الظواهر الية انتشار الصوت العادي، التي تتلخص غي انضغاط وتخلخل المادة برفقة الحقل المغنطيسي المتجمد فيها ويمكن ايجاد سرعة الانتشار من العلاقة العادية لسرعة الصوت. اذا وضعنا الضغط المغنطيسي H2 /8 π  الى جانب ضغط الغاز p على قدم المساواة عندئذ تعطى سرعة انتشار الموجة الصوتية – المغنطيسية بالعلاقة التالية:

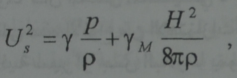
حيث p = n_iM- كثافة البلازما،   γ_M ، γ  قرينتا الكظم من اجل الضغطين العادي والمغنطيسي واما قرينة الكظم من اجل الضغط المغنطيسي فتساوي =2γ_M وهذا ما يمكن اي استنتاجه سواء من اعتبارات ميكروسكوبية (مجهرية) او من اعتبارات ماكروسكوبية(جهرية).

فمن وجهة النظر الميكروسكوبية لا يؤثر الحقل المغنطيسي الا على المركبة العرضية لحركة الجسيمة، وذلك في مستو يعامد هذا الحقل، وللحركة العرضية درجتا حرية ومن اجل الحركة بدرجتي حرية تكون قرينة الكظم مساوية 2 . ومن وجهة نظر ماكروسكوبية تعطى قرينة الكظم بالعلاقة:

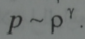
لدى الحقل المتجمد تكون الكثافة p≈H ويكون الضغط المغنطيسيH²~P² ~P_M ومن هنا ينتج ايضا ان y_M =2. وبالتعويض عن y_M بقيمتها هذه نحصل من اجل سرعة الصوت عبر اتجاه معترض على الحقل المغنطيسي على:

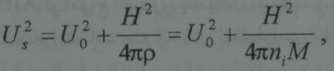
حيث U₀- السرعة العادية للصوت، المرتبطة بضغط الغاز بالعلاقة:

بادخال العلاقة بين ضغط الغاز والضغط المغنطيسي:

 nT / H²  π8= β

حيث n- التركيز الكلي لجسيمات البلازما نجد:

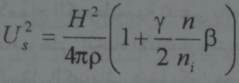
وعندما 0→β تؤول سرعة الصوت المنتشر مصالبا الحقل المغنطيسي الى الشكل:

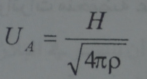
الذي هو سرعة الصوت المغنطيسي البحت في البلازما الباردة.

بوجود الحقل المغنطيسي يكتسب مفهوم البلازما الباردة معنى محددا تماما. والبلازما الباردة هي تلك البلازما التي من اجلها يكون ضغط الغاز صغبرا بالمقارنة مع الضغط أي 1>> β وعند تحقق هذا الشرط يمكن اهمال الحركة الحرارية.

وتتلخص الية الاهتزازات المنتشرة على طول منحى الحقل المغنطيسي في انحناء خطوط القوة المغنطيسية بالترافق مع البلازما الملتصقة مع هذه الخطوط . وتكون سرعة حركة المادة هنا معامدة لاتجاه الانتشار . ويمكن مقارنة الامواج الهدروديناميكية المغنطيسية هذه او امواج الففين باهتزازات الوتر. ولا يوجد في ميكانيك السائل او الغاز العادي أي تشابه معها . ولا يمكن ان توجد اهتزازات مرنة مشابهة الا في الجسم الصلب. ويمكن القول ان الحقل المغنطيسي هنا يكسب البلازما نوعا ما من المرونة. جاعلا منها الى حد ما جسما صلبا.

ومن الجدير بالذكر ان سرعة انتشار الامواج الهدروديناميكية المغنطيسية على طول منحى الحقل المغنطيسي عند تواترات منخفضة تساوي بدقة سرعة الصوت المغنطيسي في البلازما الباردة على الرغم من الالية المختلفة للظاهرة. هذه السرعة U_A تدعى سرعة الففين . ولتلافي سوء الفهم نشير الى بعض التشويش الحاصل في التسميات ففي نظرية المرونة والهدروديناميك تطلق تسمية اهتزازات طولية على الاهتزازات التي يكون فيها الانتشار موافقا لمنحى وتطلق تسمية الاهتزازات العرضية على الاهتزازات التي تتحرك فيها المادة معامدة اتجاه الانتشار . ضمن هذا المعنى الميكانيكي تعد الاهتزازت الصوتية – المغنطيسية اهتزازات طولية وتعد اهتزازات الففين اهتزازات عرضية. عندها يبدو ان الاهتزازات الطولية تنتشر وفق منحى عمودي على الحقل المغنطيسي والاهتزازت العرضية وفق منحى الحقل نفسه. ولكن الامواج الكهرطيسية تدعى بالعرضية لان الحقول الكهربائية فيها تقع في مستو متعامد على اتجاه الانتشار وتدعى الاهتزازات الكهروساكنة في البلازما بالطولية لان الحقل الكهربائي فيها يكون موجها وفق اتجاه الانتشار . وتبقى امواج الففين عرضية في مفهوم التحريك الكهربائي هذا. ولكن تبدوا الاهتزازات الصوتية – المغنطيسية عند تواترات منخفضة عرضية ايضا في تقريب اولي.

_______________________________

(1) اذا ما اخذت الحركة الحرارية بالاعتبار فانه بجوار التواترات السيكلترونية ومدرجاتها تنشأ بعض الخصوصيات.

مواضيع ذات صلة

الانتثار ثنائي القطبية

عمليات النقل في الحقل المغناطيسي

احلال التوازن الحراري

التصادمات الكولونية

التصادمات مع الجسيمات المعتدلة

مسار ومقطع التصادمات

العمليات العشوائية

امواج الصدم في البلازما

تخامد وحث الاهتزازات

المجاوبات البلازمية والدلائل الموجية

مرور الامواج العامة الراديوية عبر البلازما

الامواج المائلة والتصنيف العام للاهتزازات