
Quartic in Three Dimensions
 المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
المؤلف:
Sidney B. Cahn, Gerald D. Mahan And Boris E. Nadgorny
 المصدر:
A GUIDE TO PHYSICS PROBLEMS
المصدر:
A GUIDE TO PHYSICS PROBLEMS
 الجزء والصفحة:
part 2 , p 64
الجزء والصفحة:
part 2 , p 64
 19-8-2016
19-8-2016
 1621
1621
Quartic in Three Dimensions
A particle of mass m is bound in three dimensions by the quartic potential V(x) = Ar4. Use variational methods to estimate the energy of the ground state.
SOLUTION
The potential V(r) = Ar4 is spherically symmetric. In this case we can write the wave function as a radial part R(r) times angular functions. We assume that the ground state is an s-wave, and the angular functions are P0, which is a constant. So we minimize only the radial part of the wave function and henceforth ignore angular integrals. In three dimensions the integral in spherical coordinates is d3r = 4πr2 dr. The factor 4π comes from the angular integrals. So we just evaluate the r2 dr part. Again we choose the trial function to be a Gaussian:
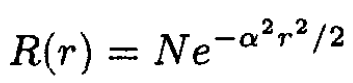 (1)
(1)
have a slightly different form in three dimensions:
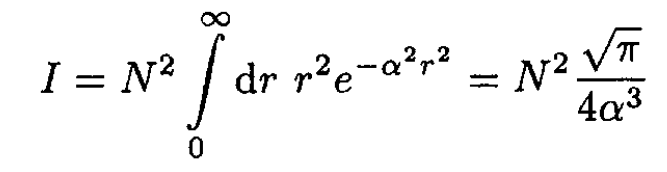 (2)
(2)
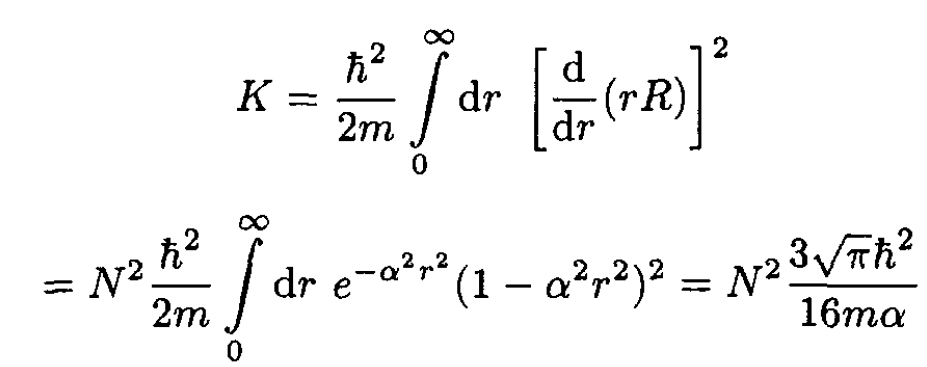 (3)
(3)
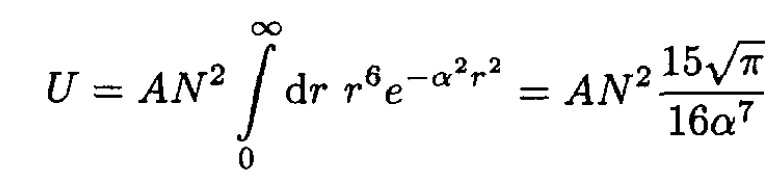 (4)
(4)
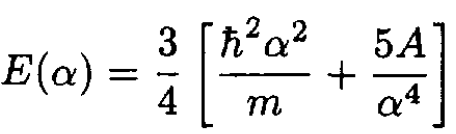 (5)
(5)
Note the form of the kinetic energy integral K, which again is obtained from Rp2 R by an integration by parts. Again set the derivative of E(α) equal to zero. This determines the value α0 which minimizes the energy:
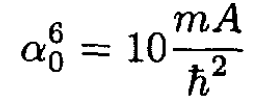 (6)
(6)
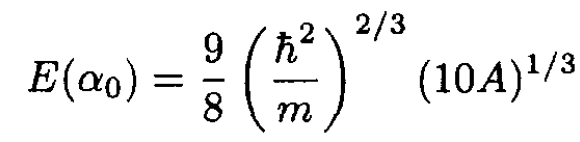 (7)
(7)
 الاكثر قراءة في مواضيع اخرى
الاكثر قراءة في مواضيع اخرى
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة


