المحددات-خواص دالة المحدد
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
106-110
8-3-2016
10774
خواص دالة المحدد:
يتضمن هذا البند بعض الخواص المهمة لدالة المحدد .
الخاصية الأولى:
لتكن A مصفوفة سعتها n × n و k عدد ثابت فإن:
البرهان: بما أن كل عامل مشترك في أي صف من صفوف A يمكن إخراجه خارج المحدد (مبرهنة 2-3-3(1)) ولما كان عدد صفوف A هو n وإن كل صف فيه عامل مشترك k فإن:
|KA|=Kn|A|
مثال (1):
البرهان:
سنوضح العلاقة أعلاه بمثال:
مثال (2):
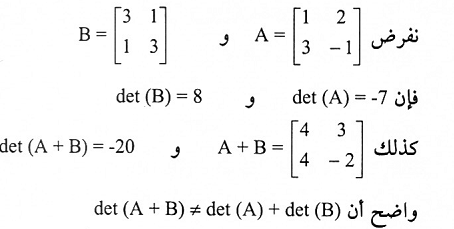
الخاصية الثالثة:
لتكن A و B مصفوفتان مربعتان لوهما نفس السعة فإن:
البرهان:
ليس من السهولة برهان هذه الخاصية، إذ يجب معرفة بعض النتائج الإضافية. لذا سنكتفي بمثال توضيحي.
نفرض A و B مصفوفتان سعة كل منهما 2 × 2حيث:
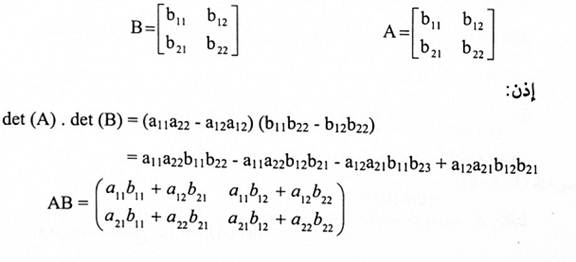
لذا:
مثال(3):
مبرهنة (1-1):
المصفوفة المربعة A قابلة للانعكاس إذا وفقط إذا det(A)≠0
البرهان:
نفرض أن A قابلة للانعكاس أي أن AA-1 = 1 إذن
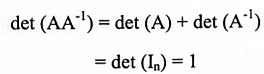
ومن هنا نستنتج أن : det (A) ≠ 0
وبالعكس نفرض det (A) = 0 ولتكن S هي الشكل المدرج الصفي للمصفوفة A.
بما ان S يمكن الحصول عليها بواسطة سلسلة منتهية من العمليات الصفية البسيطة أي يمكننا إيجاد مصفوفات بسيطة En, … , E2, E1 بحيث:
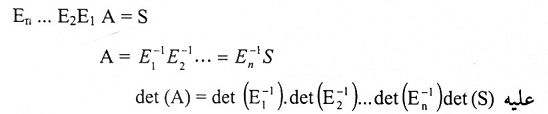
وبما أن det (A) = 0 فإنdet (S) ≠ 0 هذا يعني أن الشكل المدرج الصفي المختزل S لا يحتوي على أس صف جميع عناصره أصفار. لذا فإن S = I إذن معكوس المصفوفة A موجود ويساوي
A-1=En…..E2E1
الخاصية الرابعة:
إذا كانت A مصفوفة قابلة للانعكاس سعتها n × n فإن
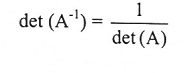
البرهان:
بما أن AA-1 = I فإن det (A-1A) det (I)
ينتج من ذلك : det (A-1). det (A) = 1
ولما كان det (A) ≠ 0
مبرهنة (1-2):
لتكن A مصفوفة سعتها n × n فإن الصيغ الآتية متكافئة.
1. A قابل للانعكاس.
2. AX = 0 له حل واحد فقط هو الحل الصفري.
3. الشكل المدرج الصفي المختزل للمصفوفة A هو In.
4. A تكتب كحاصل ضرب عدد محدد من المصفوفات الاولية.
5. AX = B نظاماً متسقاً لكل B ذات السعة n x 1 .
6. AX = B له بالضبط حل واحد لكل B ذات السعة n x 1.
الاكثر قراءة في الجبر الخطي
اخر الاخبار
اخبار العتبة العباسية المقدسة
