اقطرة المصفوفة
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
359-369
1-3-2016
10496
سنركز اهتمامنا في هذا البند على إيجاد أساس Rn المتكون من المتجهات الذاتية للمصفوفة A ذات السعة n x n، ومن ثم توظيفها في العلوم التطبيقية.
تعريف (1-1):
يقال للمصفوفة المربعة A بأنها قابلة للأقطرة إذا وجدت مصفوفة مثل P قابلة للانعكاس بحيث:
P-1AP=D
حيث D مصففة قطرية. P تسمى مؤقطرة A.
مثال(1):
حول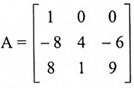 
إلى مصفوفة قطرية.
1. نوجد المعادلة المميزة.
3. بالتعويض في المعادلة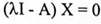 
واختزال المصفوفة الناتجة ومن ثم بحل النظام المتجانس نحصل على:
5. إذن عند تعويض 
بالتعويض عن a = -16 (لأن a كمية ثابتة ويمكن اختيارها -16).
وعند التعويض عن λ=6والضرب c = 1 نحصل على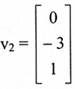 
واخيراً عند تعويض 7 =λو v = 1 نحصل على المتجه الذاتي 
6. بوضع الأعمدة v3, v2, v1 بشكل صفوف نحصل على المصفوفة التالية:
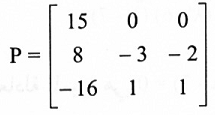
بما أن P قابلة للانعكاس ، نجد P-1 بإحدى الطرق التي تعلمناها في فصول سابقة.
7. وبالتعويض في العلاقة P-1AP سنحصل على
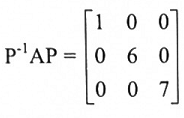
لاحظ أن عناصر القطر الرئيسي في D هي القيم الذاتية للمصفوفة A وكما وأن صفوف P هي المتجهات الذاتية v3, v2, v1
مبرهنة (1-2):
إذا كانت A مصفوفة سعتها n x n، فإن A قابلة للأفطرة إذا وفقط إذا احتوي على n من المتجهات الذاتية المستقلة خطياً وأن صفوف P هي المتجهات الذاتية المستقلة خطياً.
البرهان:
نفرض أن A تحوي على n من المتجهات الذاتية المستقلة خطياًvn , …., v2, v1 المرافقة للقيم الذاتية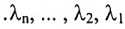 
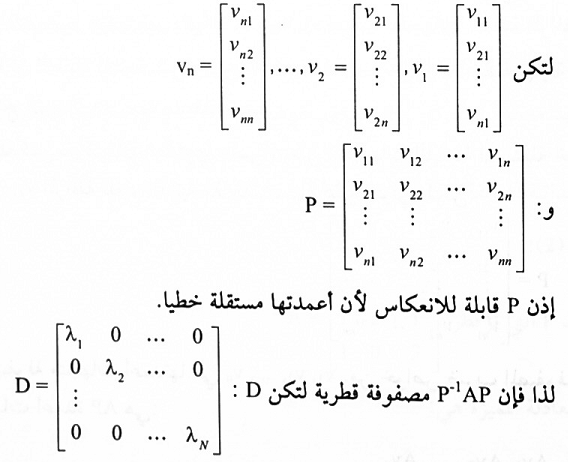
إذن P-1AP = D ، أي أن AP = PD.
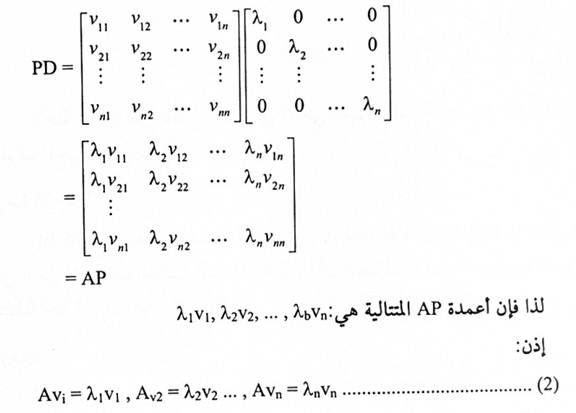
حيث D مصفوفة قطرية قيمها الذاتية,λ1 n,…. ,λ2λ بما أن متجهات أعمدة P مستقلة خطياً، فإن P قابلة للانعكاس بموجب (3) فإن P-1AP = D، بمعنى آخر، A قابلة للأقطرة.
ويمن تلخيص طريقة أقطرة المصفوفة A كما يأتي:
1. نجد المتجهات الذاتية للمصفوفة A المستقلة خطياً، نسميها v2, v1, …, vn.
2. نكون المصفوفة P، أي P-1 ومن ثم نعوض في P-1AP والتي ستكون مصفوفة قطرية عناصرها في القطر الرئيسي هي: 
هي القيم الذاتية المرافقة للمتجهات الذاتية vn, …, v2, v1.
مثال(2):
أوجد P التي تؤقطر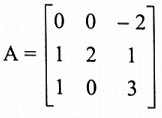 
1. المعادلة المميزة هي:
2. القيم وبما أن هذه المتجهات مستقلة خطياً لذا فإنها تؤلف أساس للفضاء الذاتي المرافق.
وعندما λ =1فإن (4) تصبح:
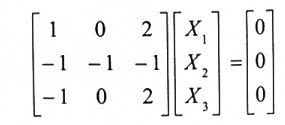
وبحل هذا النظام نحصل على:
X3 = a , a2 = a , x1 = -2a
عليه فإن المتجهات الذاتية المرافقة لــ 1= λهي متجهات غير صفرية وبالشكل:
لهذا أصبح لدينا ثلاث متجهات هي الأساس وعليه فإن A قابلة للأقطرة
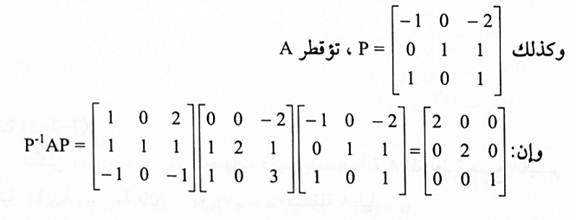
مثال(3):
أوجد P التي تؤقطر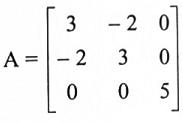 
القيم الذاتية لــA هي: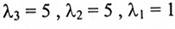 
والمتجهات الذاتية المرافقة والمستقلة خطياً هي:
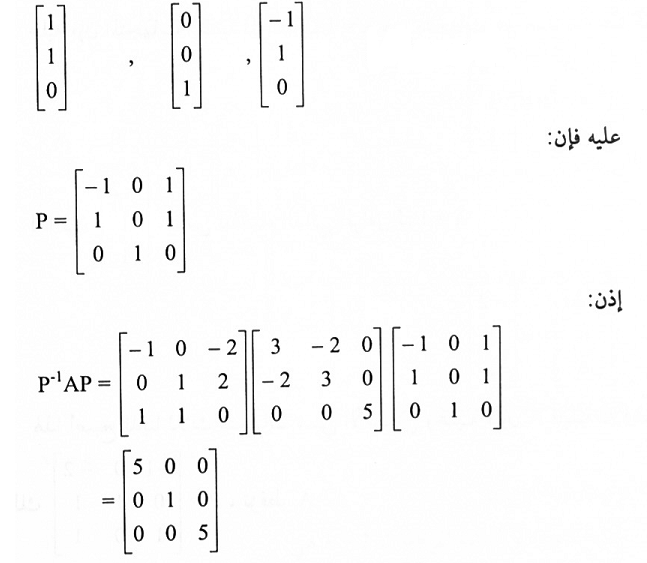
مبرهنة (1-3):
لتكن vn, … v2, v1
متجهات ذاتية للمصفوفة A المترافقة مع القيم الذاتية 
فإن vn, …, v2, v1 مستقلة خطياً.
البرهان:
1. نفرض m =2
بضرب طرفي المعادلة (5) بالمصفوفة A نحصل على:
2. نفرض أن المبرهنة صحيحة عندما m = k (بمعنى أن k من المتجهات الذاتية، مستقلة خطياً).
3. الآن نفرض m = k + 1
إذن c1 = c2 = …. ck
وهذا يعني أن ck+1 = 0
مبرهنة (1-4):
إذا كانت vn ,… , v2, v1 متجهات ذاتية مرافقة للقيم الذاتية 
فإن A قابلة للأقطرة.
البرهان:
بما أن vn , …. , v2, v1 متجهات ذاتية فإن مبرهنة (7-2-3) تبين لنا أن vn , …. , v2, v1 مستقلة خطياً. لذا فإن A قابلة للأقطرة حسب مبرهنة (1-2).
حساب قوى المصفوفة A:
لتكن A مصفوفة سعتها n x n و P مصفوفة قابلة للانعكاس فإن:
مثال(4):
أوجد A10 حيث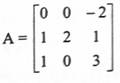 
الحل:
الاكثر قراءة في الجبر الخطي
اخر الاخبار
اخبار العتبة العباسية المقدسة
