التحويلات الخطية العامة والمصفوفات
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
405-413
29-2-2016
13202
في هذا البند سنبين أنه إذا كانت V و W فضاءات متجهات وذات أبعاد منتهية ليس ضرورياً أن يكون Rn أو Rm، فإن أي تحويل خطي T:V⟶W يمكن اعتباره تحويل مصفوفي. إن الفكرة الأساسية هي في اختيار أساسات للفضاءات V و W والتعامل معها على أساس كونها إحداثية للمتجهات عوضاً عن المتجهات نفسها.
نفرض أن بعد v هو n وبعد w هو m وكذلك أساس V هو B وأساس W هو C . لذا لكل متجه x في V المصفوفة الإحداثية B[X] هي متجه في R" والمصفوفة الإحداثية [T(X)] ستكون متجه في Rm. الشكل أدناه يوضح هذه الأفكار.
شكل (1-1)
وإذا أكملنا الشكل المستطيل أعلاه سنحصل على تطبيق (دالة) من Rn إلى Rm والتي يمكن إثباتها بأنها تحويلة خطية. فلو افترضنا أن A هي المصفوفة العامة لهذه التحويلة، فإن:
المصفوفة A يقال لها مصفوفة T نسبة للأساسين B و C، لاحظ الشكل
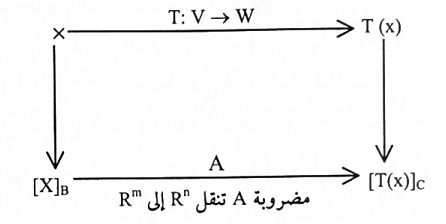
شكل (1-2)
سنوضح بعد ذلك بعض استخدامات المصفوفة A في العلاقة (1)، ولكن قبل ذلك سنين كيف نكون A.
نفرض {v1, v2, … , vn} =B أساس V و {u1 , u2, …, un}=C أساس W وليكن:
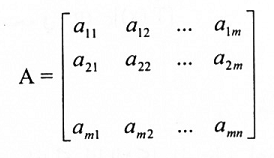
بحيث تتحقق العلاقة (1) لكل x∊V بمعنى آخر نريد تحقيق هذه العلاقة لمتجهات الأساس vn, … , v2,v1 ، أي:
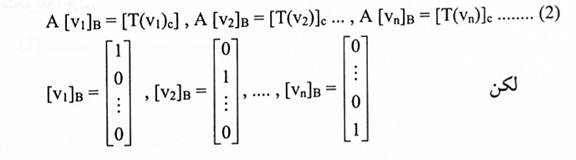
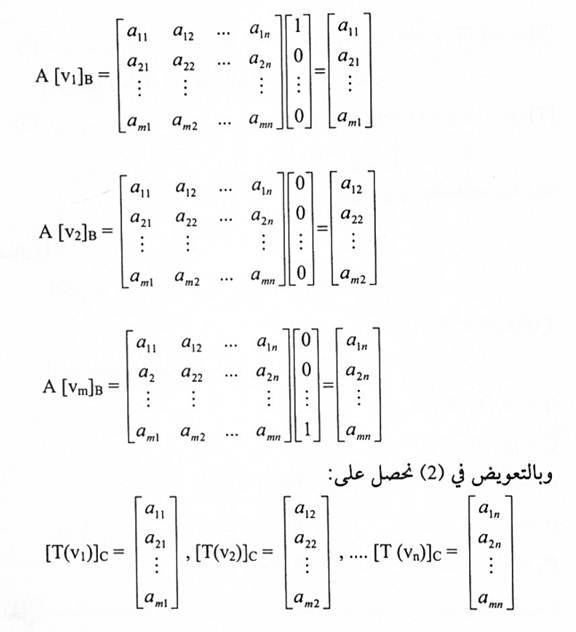
ملاحظة:
الأعمدة المتتالية للمصفوفة A هي مصفوفات إحداثية. لــ:
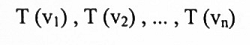
نسبة للأساس C.
لذا فإن مصفوفة T نسبة للأساسات C, B هي:
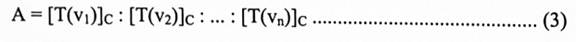
سنرمز لهذه المصفوفة بالرمز C, B[T]. لذا فإن العلاقة (3) تكتب بالشكل:
مثال(1):
الحل:
ملاحظة:
عندما V = W فإن T:V⟶W تسمى عملية خطية وفي مثل هذه الحالة B = C عند إيجاد مصفوفة T. يقال للمصفوفة T مصفوفة T نسبة إلى B وتكتب B[T] بدلاً من TB.C. إذا فرضنا أن {v1, v2, …, vn} =B إن الصيغ (4) و (5) تأخذ الصيغ الآتية
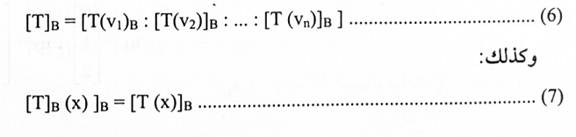
لاحظ أن العلاقتين (6) و (7) تنصان على أن مصفوفة T مضروبة في مصفوفة إحداثيات x هي مصفوفة إحداثيات T(x).
مثال (3):
مثال(4):
لاحظ أن النتيجة في الخطوة (3) هي نفسها في الخطوة (2).
الاكثر قراءة في الجبر الخطي
اخر الاخبار
اخبار العتبة العباسية المقدسة
