معكوس التحويلات الخطية
المؤلف:
علي جاسم التميمي
المصدر:
مقدمة في الجبر الخطي
الجزء والصفحة:
398-403
29-2-2016
7016
سنعمم في هذا البند المفاهيم الواردة في التحويلات الخطية T=Rn⟶Rm على التحويلات الخطية العامة.
تعريف (1-1):
يقال التحويلة T:V⟶W بأنها متباينة وتكتب (1,-1) او (one – to – one)، إذا كان كل متجه في المدى W هو صورة لمتجه واحد فقط في المنطلق V.
يمكن التعبير عن خاصية التباين جبرياً بالشكل:
إذا كانت T(v1) = T(v2) فإن v1 = v2 لكل V∊,v2 v1.
خواص التحويلات الخطية T:V⟶W
لتكن T:V⟶W تحويلة خطية فإن الخواص الآتية متكافئة:
1. متباينةT .
2. نواة T تحتوي على المتجه الصفري فقط. أي انها تحتوي على المتجه الصفري فقط. أي أن Ker T = 0
3. صفري T تساوي صفر. أي null (T) = 0
من السهولة برهان أن الخواص الثلاثة متكافئة. فإذ فرضنا أن T متباينة و v∊ker T فإن T(v) = 0 ولكن T(0) = 0 فإن v = 0 (لأن T متباينة) وعليه فإن نواة T تتكون من عنصر واحد هو العنصر الصفري [أي {0} Ker T =].
نفرض الآن أن Ker T = 0 و T(v1) = T(v2)
T(v1) – T(v2) = T(v1 – v2) [لأن Ker T ∊v1,v2]
إذن T(v1 - v2) = 0
عليه T v1-v2∊ker ومن هذا نستنتج أن T متباينة.
إذن (1) تكافئ (2) تكافئ (1).
نفرض (2) صحيحة. أي، Ker (T) = 0.
لما كان Ker T تحتوي على العنصر الصفري فإن بعد صفرية T يساوي صفر.
والآن نفرض (3) صحيحة. أي، صفرية T
تساوي صفر، بمعنى آخر
Null (T) = 0 لذا فإن بعد نواة T يساوي صفر.
عليه فإن Ker (T) يحتوي فقط على المتجه الصفري.
مثال(1):
أوجد بعد المدى وبعد نواة TA
الحل:
الشكل المدرج الصفي المختزل للمصفوفة A هي:
لإيجاد null (A) يجب أن نوجد بعد فضاء الحل للنظام الخطي المتجانس AX = 0 وبحل هذا النظام باختزال المصفوفة الممتدة للشكل المدرج السفي المختزل، سنحصل على المعادلات الآتية:
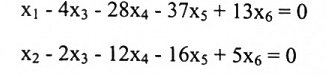
وبحل المعادلات أعلاه سنحصل على الحل العام للنظام وهو:
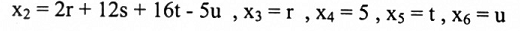
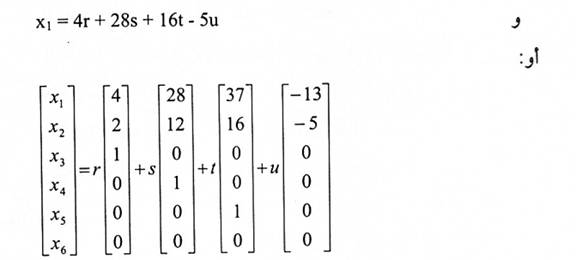
إذن المتجهات الأربعة هي أساس فضاء الحل. لذا فإن rank (A) = 2 و null(A) = 4 وبموجب المبرهنة (6-2-3) فإن rank (TA) = 2 و null (TA) = 4
مثال(2):
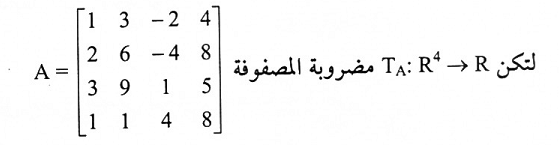
فإن TA ليست متباينة لأن A غير قابلة للانعكاس وذلك لأن محددها يساوي صفر لكون الصفين الأول والثاني أحدهما مضروب الآخر.
معكوس التحويلة الخطية العامة:
سبق وأن عرفنا معكوس العملية الخطية المتباينة Rn⟶TA:Rn. ولاحظنا أنه إذا كانت W هي صورة v تحت تأثير TA فإن TA-1 تعيد صورة w إلى v. سنحاول تعميم هذه الأفكار على العمليات الخطية العامة.
فإذا كانت T:V⟶W تحويلة خطية فإن مدى T هو فضاء جزئي من W يتكون من جميع صور المتجهات في V تحت تأثير T. إذا كانت T متباينة فإن كل متجه v في V يمتلك صورة وحيدة w = T(v) في مدى T. وحدانية الصورة هذه تساعدنا في تعريف معكوس T، يكتب T-1، التي تعيد الصور w إلى v، لاحظ الشكل (8-4).
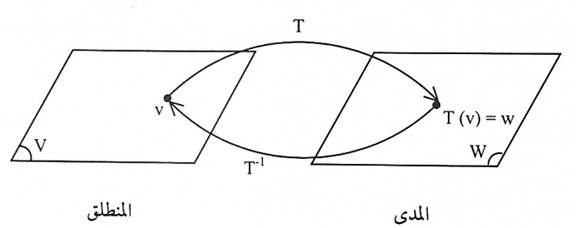
شكل (1-1)
مثال(3) :
لتكن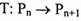 
تحويلة خطية معرفة بالشكل:
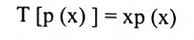
حيث P(x) متعددة حدود من الدرجة n أوجد T-1
الحل:
واضح أن T متباينة وعليه فإن T لها معكوس. كذلك:
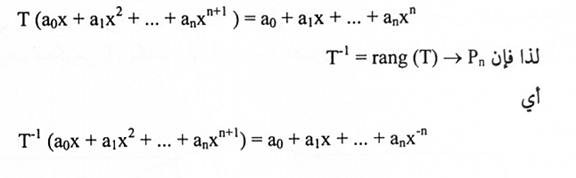
مثال(4):
إذا كان R3⟶T:R3. تحويلة خطية معرفة بالشكل
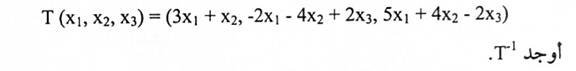
الحل:
الاكثر قراءة في الجبر الخطي
اخر الاخبار
اخبار العتبة العباسية المقدسة
