
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
الحالة الغازية
المؤلف:
بيتر أتكينز
المصدر:
الكيمياء الفيزيائية
الجزء والصفحة:
ص 57 – ص 63
2024-10-01
1779
يسهل على عالم الكيمياء الفيزيائية التعامل مع الحالة الغازية للمادة. فهذه الحالة هي الأسهل من حيث إمكانية وصفها وإجراء توقعات كمية حيالها في الحقيقة، يمكن اعتبار دراسة الغازات نقطة انطلاق أخرى للكيمياء الفيزيائية، مع روبرت بويل (1627– 1691) ودراسته لـ « مرونة الهواء» بأكسفورد في عام 1660 تقريبًا. وقد لاقت دراسة الغازات تشجيعًا أكبر من خلال دراسة سمة أخرى لطالما كانت موجودة على مدى قرون عندما حلق الإنسان في الهواء بواسطة المناطيد واعتمدت التطورات التكنولوجية في هذا الشأن على المزيد من الأبحاث الأساسية. وأذكر هنا جاك شارل (1746–1823)، ومحاولته للطيران في عام 1783، والصياغة اللاحقة لقانونه على يد كيميائي رائد آخر مهتم بالمناطيد، ألا وهو جوزيف لوي جي – لوساك (1778–1850)، في عام 1802.
حدد بويل وشارل وجي لوساك على نحو مشترك خواص المادة بحجمها الطبيعي التي تميز ما نعرفه باسم «الغاز المثالي» (أو «الغاز الكامل»)، الذي هو جوهر الحالة الغازية بالأساس. كانت تجاربهم بسيطة وأولية، تغاضت عن الفروق الدقيقة التي تميز غاز عن آخر في ظل عدم دقة قياساتهم. كانت هذه خطوة جيدة في ذلك العصر البدائي للعلم؛ إذ أمكنهم تعريف القوانين البسيطة دون الالتفات إلى الفروق الصغيرة التي أمكن التعامل معها في وقت لاحق. هكذا، أوضح بويل العلاقة بين حجم الغاز وضغطه p/1) (V ∝ ووضع شارل وجي–لوساك العلاقة بين الحجم وما نعرفه الآن بدرجة الحرارة المطلقة (V ∝ T) وعلى هذا المنوال، أضاف أميديو أفوجادرو (1776–1856) إسهاما أخيرًا؛ عندما افترض أن الأحجام المتساوية للغازات الموجودة في نفس درجة الحرارة والضغط تحتوي على عدد متساو من الجزيئات. بعبارة أخرى، يتناسب حجم الغاز مع عدد الجزيئات الموجودة (V ∝ N) تناسبًا طرديا. وهكذا، فإنه من خلال الجمع بين هذه الملاحظات، وضع «قانون الغاز المثالي»، الذي ينص على الآتي: V ∝ NkT/p. بيد أن المثير في هذا الأمر أن ثابت التناسب العام المفقود في هذه العلاقة، والمقصود بالعام هنا أنه نفس الثابت لجميع الغازات بغض النظر عن هويتها، هو ثابت بولتزمان، k، الذي عرضتُ له في الفصل الثالث، ليكون القانون كما يلي: V = NkT/p. وظهور ثابت بولتزمان هنا هو علامة أخرى على الوجود المطلق الضمني لتوزيع بولتزمان في وصف المادة، وسأتطرق إلى سبب ظهوره في هذا السياق بعد قليل.
تعليق
تكتب العلاقة V = NkT/p في الغالب على هذه الصيغة : pV = nRT. و«ثابت الغاز»، R، مرتبط بثابت بولتزمان من خلال R = NAk، حيث إن NA هو ثابت أفوجادرو وn هو كمية المادة. إنني أحجم هنا عن إغراق المناقشة بالتعريفات، ولا أفعل ذلك إلا في أضيق الحدود.
يُعد قانون الغاز المثالي، الذي سأعيد صياغته الآن على النحو التالي: p = NkT/V، من خلال ضرب كلا الطرفين في p/V، مثالًا على «معادلة الحالة»، وهو تعبير يوضح إلى أي مدى يرتبط الضغط بالمتغيرات الأخرى الخاضعة لسيطرتنا، في هذه الحالة عدد الجزيئات في العينة، ودرجة الحرارة، والحجم الذي تشغله (انظر شكل 4–1). وتُعد معادلة الحالة للغاز المثالي المثال الأبسط على الإطلاق وقد وجد أن الغازات الحقيقية تخضع لها بشكل متزايد عندما يقل الضغط. وهذا يعني أن قانون الغاز المثالي هو «قانون مقيد» من منطلق أنه صحيح تمامًا فقط عند شرط معين، في هذه الحالة p→O. توصف الغازات الحقيقية في حالات الضغط غير الصفري بمعادلات حالة أعقد ليست معروفة دومًا، إلا أن لها تعبيرات تقريبية. ومع ذلك، ولحسن الحظ، فإن معادلة الغاز المثالي تعد تقريبًا جيدًا جدًّا في حالات الضغط الطبيعي، وتُستخدم على نحو واسع كنقطة انطلاق في النقاشات الخاصة بالكيمياء الفيزيائية.
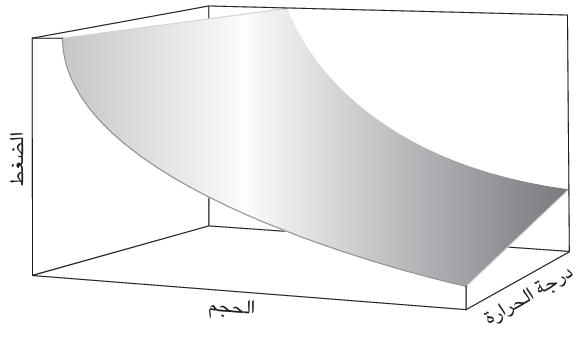
شكل 4–1: تلخص معادلة الحالة للغاز المثالي الحالات المسموح بها لهذا الغاز، وهو غاز لا تتجاذب الجزيئات فيه ولا تتنافر. ويوضح هذا الشكل قيم الضغط المسموح بها عند قيم معينة لحجم الغاز ودرجة حرارته.
إن وجود معادلة الحالة للغاز المثالي يقودني إلى جانب مهم جدًّا من الكيمياء الفيزيائية، ألا وهو: بناء النماذج. ينظر علماء الكيمياء الفيزيائية إلى العلاقات المثبتة تجريبيا (أي تلك التي بين الخواص التي أثبتتها التجارب مثل معادلة الحالة) باعتبارها تحديا: ما التفسير الجزيئي الذي يمكن التوصل إليه والذي يفسر القانون أو العلاقة المرصودة، ومن ثم كيف يمكن تعديله لتفسير الحالات الشاذة عن القانون البسيط؟ وفي حالة الغازات، يتمثل التحدي في بناء نموذج للغاز المثالي يتوافق مع معادلة الحالة للغاز المثالي المرصودة ثم تعديل النموذج بحيث تُستخلص معادلات الحالة للغازات الحقيقية. تنتشر فكرة بناء النماذج في الكيمياء الفيزيائية، ليس فقط عند وصف الغازات، وسأضرب عدة أمثلة عليها أثناء المضي قدما عبر هذه الفصول. بالطبع، يعتقد البعض أن العلوم برمتها قائمة على بناء نماذج للواقع المادي؛ وقدر كبير من الكيمياء الفيزيائية قائم على ذلك بالتأكيد.
ويعد نموذج المادة المفسر لمعادلة الحالة للغاز المثالي واحدًا من أغرب النماذج في العلوم؛ وقد نشأ من الجهل بالأساس. تقرُّ «النظرية الحركية للغازات» أننا لا نعرف حقًا أي شيء عن تفاصيل ما يحدث في أي غاز باستثناء أن الجزيئات تتحرك في حركة عشوائية متواصلة وتتعرض لتصادمات بعضها مع بعض ومع جدران الحاوية. وعند استكشاف ذلك النموذج، يتضح أن p ∝ N/V، مع وجود ثابت تناسب مرتبط بمتوسط سرعة الجزيئات في العينة. وهذا يعني أنه يمكن حساب السرعة من توزيع بولتزمان، الذي نشأ أيضًا من الجهل، الجهل بالتوزيع الفوري للجزيئات على نطاق حالات الطاقة المتاحة لها في هذه الحالة حالات الطاقة المتعلقة بحركتها الحرة عبر الفراغ. واتضح أن الثابت المفقود هو بكل بساطة kT، وبهذا نصل إلى المعادلة التالية: معادلة الحالة للغاز المثالي. ومن منطلق جهلنا بالتفاصيل المتعلقة p = NkT/V، وهي بماهية ما تقوم به الجزيئات، توصلنا إلى استنتاج جرى التحقق منه تجريبيا.
يتعين علي هنا أن أشير إلى عدة نقاط بخصوص هذا النموذج والاستنتاجات المستقاة منه. أولًا، يتجاهل النموذج حقيقة أن الجزيئات الحقيقية تتفاعل بعضها مع بعض، فتتجاذب عندما تكون قريبة وتتنافر عندما تتلامس. ونظرًا إلى أنه جرى إغفال هذا الإسهام، فإن بإمكاننا الاعتقاد أن الانحرافات التي تبديها الغازات الحقيقية عن معادلة الغاز المثالي هي بسبب هذه التفاعلات ولذا، من أجل تعزيز النموذج وتفسير حالات الانحراف عن السلوك المثالي، يجب وضع هذه التفاعلات في الحسبان. وهذه هي إحدى مهام الديناميكا الحرارية الإحصائية أو في حال إذا ما كان ذلك النهج صعبًا للغاية، يجب اقتراح طرق يمكن بها تعديل معادلة الغاز المثالي. على سبيل المثال، اقترح يوهانس فان دير فالس (1837–1923) تعديلا في عام 1873 دمجت فيه عمليات الجذب والتنافر بواسطة المعاملين a و b . يسهل فهم أحد هذين المعاملين، ألا وهو المعامل b: فهو يمثل عمليات التنافر التي تمنع أي جزيء من شغل المساحة التي يشغلها بالفعل جزيء آخر، ويقلل ببساطة الحجم المتاح للغاز؛ وبالتالي تغير عمليات التنافر المعادلة p = NkT / V إلى p = NkT / (V – b). وتلفت «معادلة حالة فان دير فالس» الناتجة (التي تشمل أيضًا حدًّا يتناسب مع المعامل a لتوضيح تأثير عمليات التجاذب بين الجزيئات) الانتباه إلى الكثير من خواص الغازات الحقيقية ويستخدمها عادةً علماء الكيمياء الفيزيائية لنمذجة سلوكها (انظر شكل 4–2).

شكل 4–2: عندما تتفاعل جزيئات الغاز بعضها مع بعض، يعتمد الضغط على الحجم بطريقة أعقد مما هو موضح في شكل 4–1.
ثانيًا، إن النموذج يمكن أن يتطور لاستنتاج بعض التفاصيل بخصوص متوسط سلوك الجزيئات في الغاز ولتقديم بعض المعلومات حول ما يحدث في أية عينة من الغاز. ومثل هذه المعلومات مهمة لفهم خواص الغازات والتفاعلات التي تخضع لها. ومن ثم، يمكن استخدام توزيع بولتزمان لحساب متوسط سرعة الجزيئات ونسبة الجزيئات التي لها سرعة محددة (انظر شكل 4–3). بالنسبة إلى الجزيئات الخفيفة (مثل جزيئات العنصرين الرئيسيين للهواء، ألا وهما N2 وO2) في درجة حرارة الغرفة، تتحرك الجزيئات بسرعة كبيرة بمتوسط سرعة يبلغ نحو 500 م / ث (أي، نحو 1000 ميل في الساعة). وتتوافق هذه السرعة مع ما نعرفه عن انتشار الصوت الذي تبلغ سرعته نحو 340 م/ث عبر الهواء لكي ينتشر الصوت، يجب على الجزيئات أن تعدل موقعها لتعطي موجة من الضغط المتذبذب، وبالتالي فإن المعدل الذي تفعل به ذلك يجب أن يكون مماثلا لمتوسط سرعاتها.

شكل 4–3: يوضح «توزيع ماكسويل – بولتزمان للسرعات» نسبة الجزيئات التي لها سرعة محددة عند درجة حرارة معينة ويمكن استخدامه لحساب متوسط سرعة الجزيئات. ولا تحظى الجزيئات الخفيفة بمتوسط سرعات عال المبين هنا بالخطوط المنقطة) وحسب؛ وإنما أيضًا تتحرك نسبة كبيرة منها بسرعة بالغة.
ويمكن تطوير النموذج الحركي لتوقع متوسط وتيرة التصادم بين الجزيئات ومتوسط المسافة التي تقطعها الجزيئات بين التصادمات. ومن أجل القيام بذلك، تُصوَّر الجزيئات الشبيهة بالنقاط التي تفترضها النظرية الأساسية على أنها محاطة بكرة ذات نصف قطر معين يعتمد على هوية الجزيئات، وتحسب «ضربة» عندما تتلامس كرتين من مثل تلك الكرات. وعند العمل على هذه الفكرة، يتضح أن أي جزيء N2 أو O2 في الهواء يُحدث تصادمًا كل نانو ثانية ويقطع نحو 1000 قطر جزيئي بين التصادمات. ولكي يتضح هذا القياس: إذا تخيلنا الجزيء بحجم كرة تنس إذن فإنه يقطع مسافة بطول ملعب التنس بين التصادمات. ويصطدم كل جزيء نحو مليار مرة في الثانية.
لقد استخدم علماء الكيمياء الفيزيائية، بالتعاون مع الفيزيائيين، النموذج الحركي لدراسة المعدل الذي تنتقل به الخواص عبر الغازات ومعدل تصادم الجزيئات على الأسطح. فعلى سبيل المثال، استطاعوا الربط بين التوصيل الحراري» الخاص بغاز ما – أي، قدرته على نقل الحرارة عبر تدرُّج درجة حرارة – والخواص الجزيئية. ويعتبر النموذج أيضًا محوريًا في دراسة معدلات حدوث التفاعلات الكيميائية في الغازات. إن كمية المعلومات التي يمكن استخلاصها من حالة الجهل شبه التام مدهشة جدًّا حقًا.
 الاكثر قراءة في الفيزياء الكيميائية
الاكثر قراءة في الفيزياء الكيميائية
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















