As our fundamental “law” of electromagnetic radiation, we are going to assume that (28.6) is true, i.e., that the electric field produced by an accelerating charge which is moving nonrelativistically at a very large distance r approaches that form. The electric field varies inversely as r and is proportional to the acceleration of the charge, projected onto the “plane of sight,” and this acceleration is not today’s acceleration, but the acceleration that it had at an earlier time, the amount of delay being a time, r/c. In the remainder of this chapter we shall discuss this law so that we can understand it better physically, because we are going to use it to understand all of the phenomena of light and radio propagation, such as reflection, refraction, interference, diffraction, and scattering. It is the central law, and is all we need. All the rest of Eq. (28.3) was written down only to set the stage, so that we could appreciate where (28.6) fits and how it comes about.

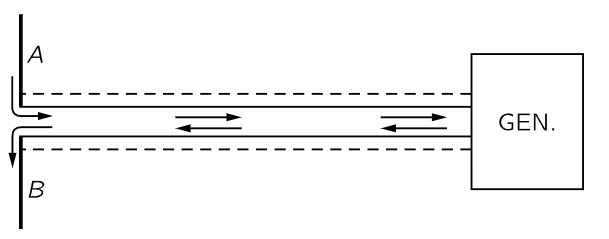
Fig. 28–1.A high-frequency signal generator drives charges up and down on two wires.

We shall discuss (28.3) further next year. In the meantime, we shall accept it as true, but not just on a theoretical basis. We may devise a number of experiments which illustrate the character of the law. In order to do so, we need an accelerating charge. It should be a single charge, but if we can make a great many charges move together, all the same way, we know that the field will be the sum of the effects of each of the individual charges; we just add them together. As an example, consider two pieces of wire connected to a generator, as shown in Fig. 28–1. The idea is that the generator makes a potential difference, or a field, which pulls electrons away from piece A and pushes them into B at one moment, and then, an infinitesimal time later, it reverses the effect and pulls the electrons out of B and pumps them back into A! So in these two wires charges, let us say, are accelerating upward in wire A and upward in wire B for one moment, and a moment later they are accelerating downward in wire A and downward in wire B. The fact that we need two wires and a generator is merely that this is a way of doing it. The net result is that we merely have a charge accelerating up and down as though A and B were one single wire. A wire that is very short compared with the distance light travels in one oscillation period is called an electric dipole oscillator. Thus, we have the circumstance that we need to apply our law, which tells us that this charge makes an electric field, and so we need an instrument to detect an electric field, and the instrument we use is the same thing—a pair of wires like A and B! If an electric field is applied to such a device, it will produce a force which will pull the electrons up on both wires or down on both wires. This signal is detected by means of a rectifier mounted between A and B, and a tiny, fine wire carries the information into an amplifier, where it is amplified so we can hear the audiofrequency tone with which the radiofrequency is modulated. When this probe feels an electric field, there will be a loud noise coming out of the loudspeaker, and when there is no electric field driving it, there will be no noise.

Because the room in which the waves we are measuring has other objects in it, our electric field will shake electrons in these other objects; the electric field makes these other charges go up and down, and in going up and down, these also produce an effect on our probe. Thus, for a successful experiment we must hold things fairly close together, so that the influences from the walls and from ourselves—the reflected waves—are relatively small. So, the phenomena will not turn out to appear to be precisely and perfectly in accord with Eq. (28.6), but will be close enough that we shall be able to appreciate the law.

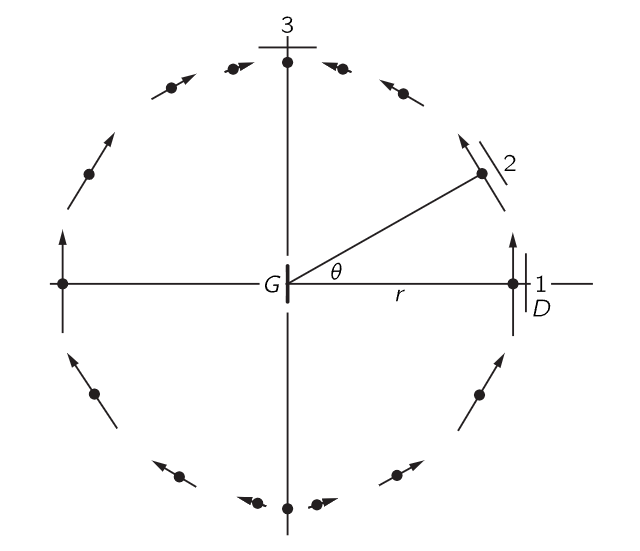
Fig. 28–2. The instantaneous electric field on a sphere centered at a localized, linearly oscillating charge.

Now we turn the generator on and hear the audio signal. We find a strong field when the detector D is parallel to the generator G at point 1 (Fig. 28–2). We find the same amount of field also at any other azimuth angle about the axis of G, because it has no directional effects. On the other hand, when the detector is at 3 the field is zero. That is all right, because our formula said that the field should be the acceleration of the charge projected perpendicular to the line of sight. Therefore, when we look down on G, the charge is moving toward and away from D, and there is no effect. So that checks the first rule, that there is no effect when the charge is moving directly toward us. Secondly, the formula says that the electric field should be perpendicular to r and in the plane of G and r; so, if we put D at 1 but rotate it 90^∘, we should get no signal. And this is just what we find, the electric field is indeed vertical, and not horizontal. When we move D to some intermediate angle, we see that the strongest signal occurs when it is oriented as shown, because although G is vertical, it does not produce a field that is simply parallel to itself—it is the projection of the acceleration perpendicular to the line of sight that counts. The signal is weaker at 2 than it is at 1, because of the projection effect.

مواضيع ذات صلة

Radiation

Electromagnetism

ثنائيات الأشعة السينية آلية عملها

انفجار الأشعة السينية المنبعثة من 1–Sco X

أستاذ المناطيد (مناطيد استكشاف الاشعة السينية)

استعادة التلسكوب الخاص باستكشاف الاشعة السينية من وسط الصحراء: جاك صائد حيوانات الكنغر

التحليق عاليا المناطيد.. وكواشف الأشعة السينية.. وعملية الإطلاق

مطاردة الأشعة السينية بالمناطيد.. البداية

ما هي الأشعة السينية؟

أشعة سينية من الفضاء الخارجي

إنجاز ماكسويل العظيم

الكهرومغناطيسية تمد يد العون