Levenberg-Marquardt Method
المؤلف:
Bates, D. M. and Watts, D. G
المصدر:
Nonlinear Regression and Its Applications. New York: Wiley, 1988.
الجزء والصفحة:
...
18-12-2021
2018
Levenberg-Marquardt Method
Levenberg-Marquardt is a popular alternative to the Gauss-Newton method of finding the minimum of a function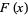 
that is a sum of squares of nonlinear functions,
Let the Jacobian of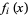 
be denoted 
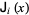, then the Levenberg-Marquardt method searches in the direction given by the solution 
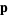to the equations
where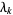 
are nonnegative scalars and 
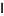is the identity matrix. The method has the nice property that, for some scalar 
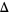related to 
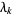, the vector 
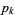is the solution of the constrained subproblem of minimizing 
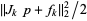subject to 
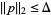(Gill et al. 1981, p. 136).
The method is used by the command FindMinimum[f, ![<span style=]()
{" src="https://mathworld.wolfram.com/images/equations/Levenberg-MarquardtMethod/Inline12.gif" style="height:15px; width:5px" />x, x0![<span style=]()
}" src="https://mathworld.wolfram.com/images/equations/Levenberg-MarquardtMethod/Inline13.gif" style="height:15px; width:5px" />] when given the Method -> LevenbergMarquardt option.
REFERENCES:
Bates, D. M. and Watts, D. G. Nonlinear Regression and Its Applications. New York: Wiley, 1988.
Gill, P. R.; Murray, W.; and Wright, M. H. "The Levenberg-Marquardt Method." §4.7.3 in Practical Optimization. London: Academic Press, pp. 136-137, 1981.
Levenberg, K. "A Method for the Solution of Certain Problems in Least Squares." Quart. Appl. Math. 2, 164-168, 1944.
Marquardt, D. "An Algorithm for Least-Squares Estimation of Nonlinear Parameters." SIAM J. Appl. Math. 11, 431-441, 1963.
الاكثر قراءة في الرياضيات التطبيقية
اخر الاخبار
اخبار العتبة العباسية المقدسة
