There are a number of equations known as the Riccati differential equation. The most common is

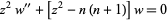(1)

(Abramowitz and Stegun 1972, p. 445; Zwillinger 1997, p. 126), which has solutions

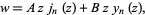(2)

where 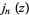 and 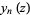 are spherical Bessel functions of the first and second kinds.

Another Riccati differential equation is

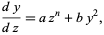(3)

which is solvable by algebraic, exponential, and logarithmic functions only when 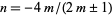, for 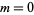, 1, 2, ....

Yet another Riccati differential equation is

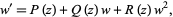(4)

where 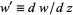 (Boyce and DiPrima 1986, p. 87). The transformation

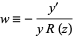(5)

leads to the second-order linear homogeneous equation

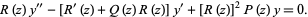(6)

If a particular solution 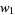 to (4) is known, then a more general solution containing a single arbitrary constant can be obtained from

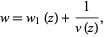(7)

where 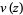 is a solution to the first-order linear equation

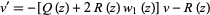(8)

(Boyce and DiPrima 1986, p. 87). This result is due to Euler in 1760.

REFERENCES:

Abramowitz, M. and Stegun, I. A. (Eds.). "Riccati-Bessel Functions." §10.3 in Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 445, 1972.

Bender, C. M. and Orszag, S. A. §1.6 in Advanced Mathematical Methods for Scientists and Engineers. New York: McGraw-Hill, 1978.

Boyce, W. E. and DiPrima, R. C. Elementary Differential Equations and Boundary Value Problems, 4th ed. New York: Wiley, 1986.

Boyle, P. P.; Tian, W.; and Guan, F. "The Riccati Equation in Mathematical Finance." J. Symb. Comput. 33, 343-355, 2002.

Glaisher, J. W. L. "On Riccati's Equation." Quart. J. Pure Appl. Math. 11, 267-273, 1871.

Goldstein, M. E. and Braun, W. H. Advanced Methods for the Solution of Differential Equations. NASA SP-316. Washington, DC: U.S. Government Printing Office, pp. 45-46, 1973.

Ince, E. L. Ordinary Differential Equations. New York: Dover, pp. 23-35 and 295, 1956.

Reid, W. T. Riccati Differential Equations. New York: Academic Press, 1972.

Simmons, G. F. Differential Equations with Applications and Historical Notes. New York: McGraw-Hill, pp. 62-63, 1972.

Zwillinger, D. (Ed.). CRC Standard Mathematical Tables and Formulae. Boca Raton, FL: CRC Press, p. 414, 1995.

Zwillinger, D. "Riccati Equation--1 and Riccati Equation--2." §II.A.75 and II.A.76 in Handbook of Differential Equations, 3rd ed. Boston, MA: Academic Press, pp. 121 and 288-291, 1997.