Asymptotic Series
المؤلف:
Abramowitz, M. and Stegun, I. A
المصدر:
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover
الجزء والصفحة:
...
13-3-2019
3612
Asymptotic Series
An asymptotic series is a series expansion of a function in a variable 
which may converge or diverge (Erdélyi 1987, p. 1), but whose partial sums can be made an arbitrarily good approximation to a given function for large enough 
. To form an asymptotic series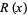 
of
 |
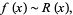(1)
|
take
![x^nR_n(x)=x^n[f(x)-S_n(x)],](http://mathworld.wolfram.com/images/equations/AsymptoticSeries/NumberedEquation2.gif) |
(2)
|
where
 |
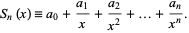(3)
|
The asymptotic series is defined to have the properties
 |
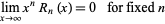(4)
|
 |
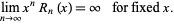(5)
|
Therefore,
 |
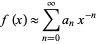(6)
|
in the limit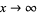 
. If a function has an asymptotic expansion, the expansion is unique. The symbol 
is also used to mean directly similar.
Asymptotic series can be computed by doing the change of variable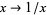 
and doing a series expansion about zero. Many mathematical operations can be performed on asymptotic series. For example, asymptotic series can be added, subtracted, multiplied, divided (as long as the constant term of the divisor is nonzero), and exponentiated, and the results are also asymptotic series (Gradshteyn and Ryzhik 2000, p. 20).
REFERENCES:
Abramowitz, M. and Stegun, I. A. (Eds.). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing. New York: Dover, p. 15, 1972.
Arfken, G. "Asymptotic of Semiconvergent Series." §5.10 in Mathematical Methods for Physicists, 3rd ed. Orlando, FL: Academic Press, pp. 339-346, 1985.
Bleistein, N. and Handelsman, R. A. Asymptotic Expansions of Integrals. New York: Dover, 1986.
Boyd, J. P. "The Devil's Invention: Asymptotic, Superasymptotic and Hyperasymptotic Series." Acta Appl. Math. 56, 1-98, 1999.
Copson, E. T. Asymptotic Expansions. Cambridge, England: Cambridge University Press, 1965.
de Bruijn, N. G. Asymptotic Methods in Analysis. New York: Dover, pp. 3-10, 1981.
Dingle, R. B. Asymptotic Expansions: Their Derivation and Interpretation. London: Academic Press, 1973.
Erdélyi, A. Asymptotic Expansions. New York: Dover, 1987.
Gradshteyn, I. S. and Ryzhik, I. M. "Asymptotic Series." §0.33 in Tables of Integrals, Series, and Products, 6th ed. San Diego, CA: Academic Press, p. 20, 2000.
Morse, P. M. and Feshbach, H. "Asymptotic Series; Method of Steepest Descent." §4.6 in Methods of Theoretical Physics, Part I.New York: McGraw-Hill, pp. 434-443, 1953.
Olver, F. W. J. Asymptotics and Special Functions. New York: Academic Press, 1974.
Wasow, W. R. Asymptotic Expansions for Ordinary Differential Equations. New York: Dover, 1987.
Weisstein, E. W. "Books about Asymptotic Series." http://www.ericweisstein.com/encyclopedias/books/AsymptoticSeries.html.
الاكثر قراءة في المتتاليات-المتسلسلات
اخر الاخبار
اخبار العتبة العباسية المقدسة
