The Kronig-Penney Model

In the previous section, we discussed qualitatively the spitting of allowed electron energies as atoms are brought together to form a crystal. The concept of allowed and forbidden energy bands can hc developed more rigorously by considering quantum mechanics and Schrodinger's wave equation. It may be easy for the reader to "get lost" in the following derivation, but the result forms the basis for the energy-band theory of semiconductors.

The potential function of a single, noninteracting, one-electron atom is shown in Figure 1.1a. Also indicated on the figure are the discrete energy levels allowed for the electron. Figure 1.1b shows the same type of potential function for the case when several atoms are in close proximity arranged in a one-dimensional array. The potential functions of adjacent atoms overlap, and the net potential function for this case is shown in Figure 1.1c. It is this potential function we would need to use in Schrodinger's wave equation to model a one-dimensional single-crystal material.

The solution to Schrodinger's wave equation, for this one-dimensional single crystal lattice, is made more tractable by considering a simples potential function. Figure 1.2 is the one-dimensional Kronig-Penney model of the periodic potential function, which is used to represent a one-dimensional single-crystal lattice. We need to solve Schrodinger's wave equation in each region. As with previous quantum mechanical problems, the more interesting solution occurs for the case when E < V₀, which corresponds to a particle being bound within the crystal. The electrons are contained in the potential wells, but we have the possibility of tunneling between wells. The Kronig-Penney model is an idealized periodic potential representing a one-dimensional single crystal. but the results will illustrate many of the important features of the quantum behavior of electrons in a periodic lattice.

To obtain the solution to Schrodinger's wave equation, we make use of a mathematical theorem by Bloch. The theorem states that all one-electron wave functions,

Figure 1.1  (a) Potential function of a single isolated atom. (b) Overlapping potential functions of adjacent atoms. (c) Net potential function of a one-dimensional single crystal.

Figure 1.2  The one-dimensional periodic potential function of the Kronig-Penney model.

for problems involving periodically varying potential energy functions, must be of the form

(1)

The parameter k is called a constant of motion and will be considered in more detail as we develop the theory. The function u(x) is a periodic function with period (a + b).

(2)

which may he written as

(3)

This traveling-wave solution represents the motion of an electron in a single-crystal material. The amplitude of the traveling wave is a periodic function and the parameter k is also referred to as a wave number.

We can now begin to determine a relation between the parameter k, the total energy E, and the potential V₀. If we consider region I in Figure 1.2 (0 < x < a ) in which V(x) = 0, take the second derivative of Equation (1), and substitute this result into the time-independent Schrodinger's wave, we obtain the relation

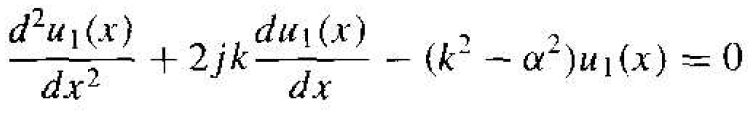(4)

The function u₁(x) is the amplitude of the wave function in region I and the parameter α is defined as

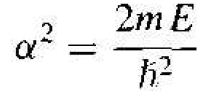(5)

Consider now a specific region II, -b < x < 0. in which V(x) = V₀, and apply Schrodinger's wave equation. We obtain the relation

(6)

where u₂(x) the amplitude of the wave t u n c tm in region II We may define

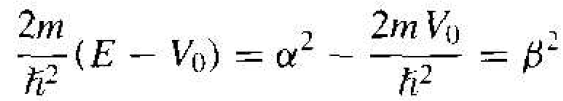(7)

so that Equation (6) may be written as

(8)

Note that from Equation (7), if E > V₀, the parameter β is real, whereas if E < V₀, then β is imaginary.

The solution to Equation (4), for region I, is of the form

(9)

and the solution to Equation (8), for region II, is of the form

(10)

Since the potential function V(x) is everywhere finite, both the wave function ѱ(x) and its first derivative ∂ѱ(x)/∂x must he continuous. This continuity condition implies that the wave amplitude function u(x) and its first derivative ∂u(x)/∂x must also he continuous.

If we consider the boundary at x = 0 and apply the continuity condition to the wave amplitude, we have

(11)

Substituting Equations (9) and (10) into Equation (11), we obtain

(12)

Now applying the condition that

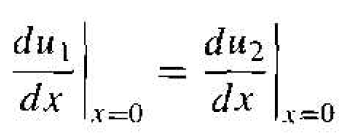(13)

we obtain

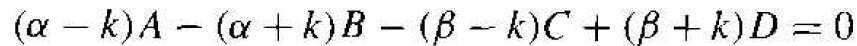(14)

We have considered region I as 0 < x < a and region II as -b < x < 0. The periodicity and the continuity condition mean that the function u₁ . as x → a . is equal to the function u₂, as x → -b. This condition may be written as

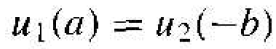(15)

Applying the solutions for u₁(x) and u₂(x) to the boundary condition in Equation (15) yields

(16)

The last boundary condition is

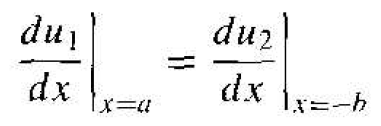(17)

which gives

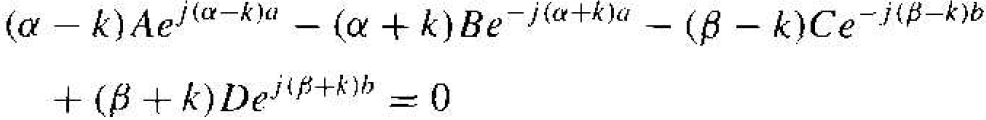(18)

We now have four homogeneous equations, Equations (12). (14), (16). And (18) with four unknowns as a result of applying the four boundary conditions. In a set of simultaneous, linear, homogeneous equations, there is a nontrivial solution if, and only if, the determinant of the coefficients is zero. In our case, the coefficients in question are the coefficients of the parameters A, B, C, and D.

The evaluation of this determinant is extremely laborious and will not he considered in detail. The result is

(19)

Equation (19) relates the parameter k to the total energy E (through the parameter α ) and the potential function V₀ (through the parameter β).

As we mentioned, the more interesting solutions occur for E < V₀, which applies to the electron bound within the crystal. From Equation (7), the parameter β is then an imaginary quantity. We may define

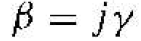(20)

where γ is a real quantity. Equation (19) can he written in terms of γ as

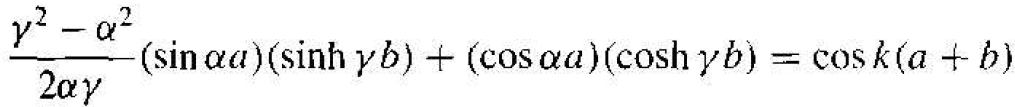(21)

Equation (21) does not lend itself to an analytical solution, but must be solved using numerical or graphical techniques to obtain the relation between k, E, and V₀.

The solution of Schrodinger's wave equation for a single bound particle resulted in discrete allowed energies. The solution of Equation (21) will result in a band of allowed energies.

To obtain an equation that is more susceptible to a graphical solution and thus will illustrate the nature of the results, let the potential barrier width b → 0 and the barrier height V₀ → ∞, but such that the product bV₀ remains finite. Equation (21) then reduces to

(22)

We may define a parameter P' as

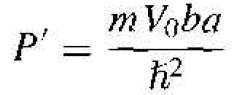(23)

Then, finally, we have the relation

(24)

Equation (24) again gives the relation between the parameter k, total energy E (through the parameter α), and the potential barrier bV₀. We may note that Equation (24) is not a solution if Schrodinger's wave equation but gives the conditions. for which Schrodinger's wave equation will have a solution. If we assume the crystal is infinitely large, then k in Equation (24) can assume a continuum of values and must be real.