


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 6-10-2020
Date: 19-12-2020
Date: 16-2-2017
|
Electrostatic energy
Consider a collection of N static point charges qi located at position vectors ri (where i runs from 1 to N). What is the electrostatic energy stored in such a collection? Another way of asking this is, how much work would we have to do in order to assemble the charges, starting from an initial state in which they are all at rest and also very widely separated? We know that a static electric field is conservative and can consequently be written in terms of a scalar potential:
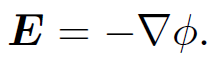 (1.1)
(1.1)
We also know that the electric force on a charge q is written
 (1.2)
(1.2)
The work we would have to do against electrical forces in order to move the charge from point P to point Q is simply
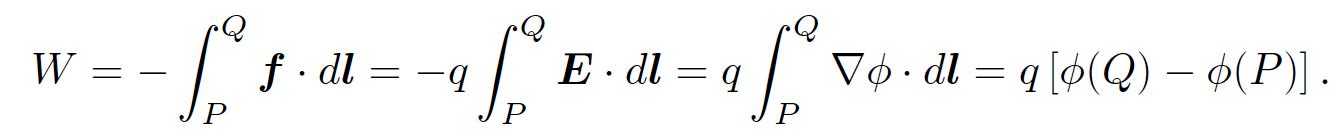 (1.3)
(1.3)
The negative sign in the above expression comes about because we would have to exert a force -f on the charge in order to counteract the force exerted by the electric field. Recall that the scalar potential generated by a point charge qʹ at position rʹ is
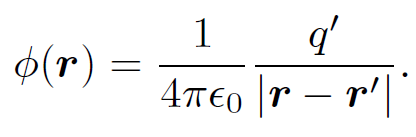 (1.4)
(1.4)
Let us build up our collection of charges one by one. It takes no work to bring the first charge from infinity, since there is no electric field to fight against. Let us clamp this charge in position at r1. In order to bring the second charge into position at r2 we have to do work against the electric field generated by the first charge. According to Eqs. (1.3) and Eqs. (1.4), this work is given by
 (1.5)
(1.5)
Let us now bring the third charge into position. Since electric fields and scalar potentials are superposable the work done whilst moving the third charge from infinity to r3 is simply the sum of the work done against the electric fields generated by charges 1 and 2 taken in isolation:
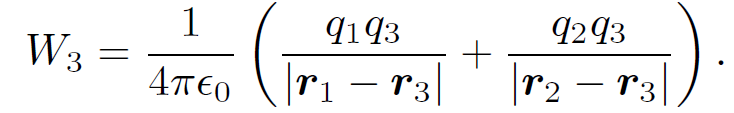 (1.6)
(1.6)
Thus, the total work done in assembling the three charges is given by
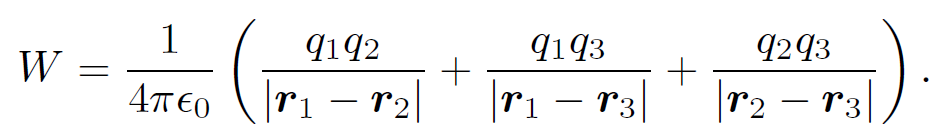 (1.7)
(1.7)
This result can easily be generalized to N charges:
 (1.8)
(1.8)
The restriction that j must be greater than i makes the above summation rather messy. If we were to sum without restriction (other than j ≠ i) then each pair of charges would be counted twice. It is convenient to do just this and then to divide the result by two. Thus,
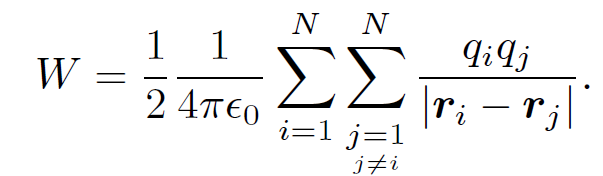 (1.9)
(1.9)
This is the potential energy (i.e., the difference between the total energy and the kinetic energy) of a collection of charges. We can think of this as the work needed to bring static charges from infinity and assemble them in the required formation. Alternatively, this is the kinetic energy which would be released if the collection were dissolved and the charges returned to infinity. But where is this potential energy stored? Let us investigate further. Equation (1.9) can be written
 (1.10)
(1.10)
where
 (1.11)
(1.11)
is the scalar potential experienced by the i th charge due to the other charges in the distribution. Let us now consider the potential energy of a continuous charge distribution. It is tempting to write
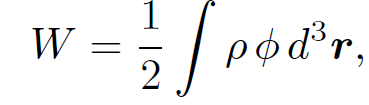 (1.12)
(1.12)
by analogy with Eqs. (1.10) and (1.11), where
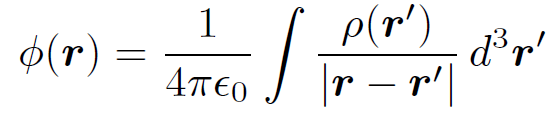 (1.13)
(1.13)
is the familiar scalar potential generated by a continuous charge distribution. Let us try this out. We know from Poisson's equation that
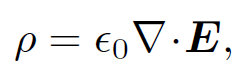 (1.14)
(1.14)
so Eq. (1.12) can be written
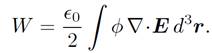 (1.15)
(1.15)
Vector field theory yields the standard result
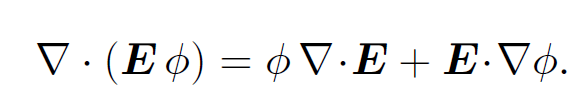 (1.16)
(1.16)
However, ∇ϕ = -E, so we obtain
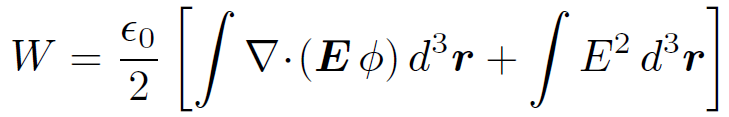 (1.17)
(1.17)
Application of Gauss' theorem gives
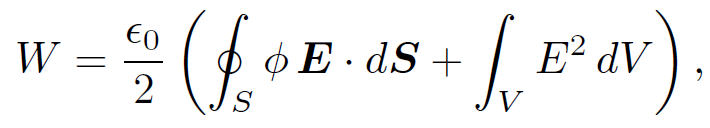 (1.18)
(1.18)
where V is some volume which encloses all of the charges and S is its bounding surface. Let us assume that V is a sphere, centred on the origin, and let us take the limit in which radius r of this sphere goes to infinity. We know that, in general, the electric field at large distances from a bounded charge distribution looks like the field of a point charge and, therefore, falls off like 1/r2. Likewise, the potential falls off like 1/r. However, the surface area of the sphere increases like r2. It is clear that in the limit as r → ∞ the surface integral in Eq. (1.18) falls off like 1/r and is consequently zero. Thus, Eq. (1.18) reduces to
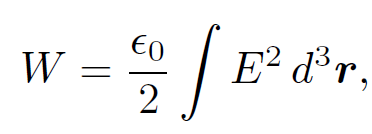 (1.19)
(1.19)
where the integral is over all space. This is a very nice result! It tells us that the potential energy of a continuous charge distribution is stored in the electric field. Of course, we now have to assume that an electric field possesses an energy density
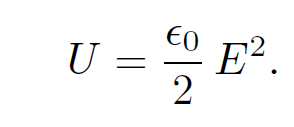 (1.20)
(1.20)
We can easily check that Eq. (1.19) is correct. Suppose that we have a charge Q which is uniformly distributed within a sphere of radius a. Let us imagine building up this charge distribution from a succession of thin spherical layers of infinitesimal thickness. At each stage we gather a small amount of charge from infinity and spread it over the surface of the sphere in a thin layer from r to r + dr. We continue this process until the final radius of the sphere is a. If q(r) is the charge in the sphere when it has attained radius r, the work done in bringing a charge dq to it is
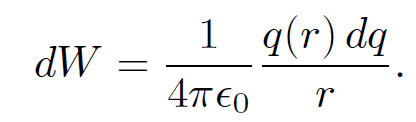 (1.21)
(1.21)
This follows from Eq. (1.5) since the electric field generated by a spherical charge distribution (outside itself) is the same as that of a point charge q(r) located at the origin (r = 0). If the constant charge density in the sphere is ρ then
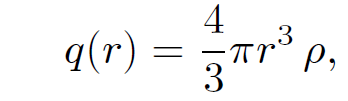 (1.22)
(1.22)
and
 (1.23)
(1.23)
Thus, Eq. (1.21) becomes
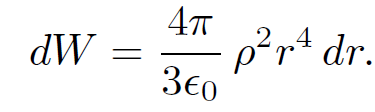 (1.24)
(1.24)
The total work needed to build up the sphere from nothing to radius a is plainly
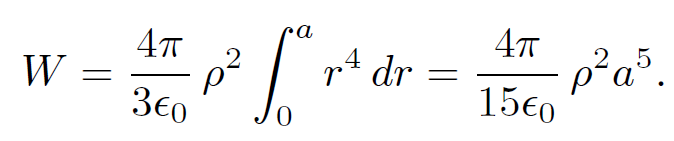 (1.25)
(1.25)
This can also be written in terms of the total charge Q = (4/3)πa3ρ as
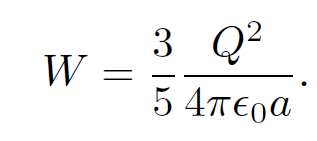 (1.26)
(1.26)
Now that we have evaluated the potential energy of a spherical charge distribution by the direct method, let us work it out using Eq. (1.19). We assume that the electric field is radial and spherically symmetric, so 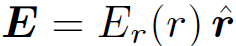 . Application of Gauss' law
. Application of Gauss' law
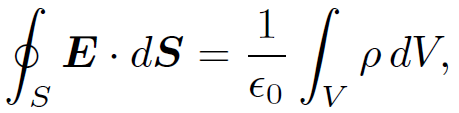 (1.27)
(1.27)
where V is a sphere of radius r, yields
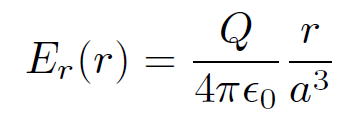 (1.28)
(1.28)
for r < a, and
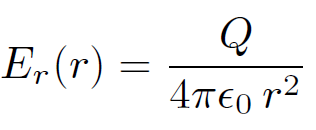 (1.29)
(1.29)
for r ¸ a. Note that the electric field generated outside the charge distribution is the same as that of a point charge Q located at the origin, r = 0. Equations (1.19), (1.28), and (1.29) yield
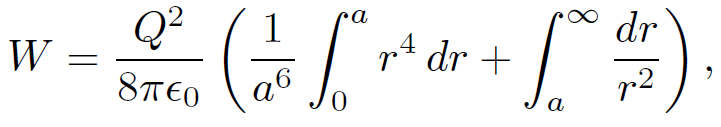 (1.30)
(1.30)
which reduces to
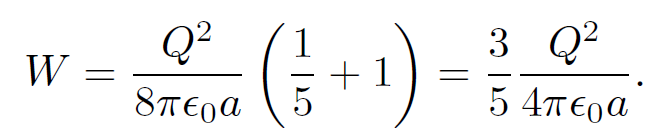 (1.31)
(1.31)
Thus, Eq. (1.19) gives the correct answer. The reason we have checked Eq. (1.19) so carefully is that on close inspection it is found to be inconsistent with Eq. (1.10), from which it was supposedly de- rived! For instance, the energy given by Eq. (1.19) is manifestly positive definite, whereas the energy given by Eq. (1.10) can be negative (it is certainly negative for a collection of two point charges of opposite sign). The inconsistency was introduced into our analysis when we replaced Eq. (1.11) by Eq. (1.13). In Eq. (1.11) the self-interaction of the i th charge with its own electric field is excluded whereas it is included in Eq. (1.13). Thus, the potential energies (1.10) and (1.19) are different because in the former we start from ready made point charges whereas in the latter we build up the whole charge distribution from scratch. Thus, if we were to work out the potential energy of a point charge distribution using Eq. (1.19) we would obtain the energy (1.10) plus the energy required to assemble the point charges. What is the energy required to assemble a point charge? In fact, it is infinite! To see this let us suppose, for the sake of argument, that our point charges are actually made of charge uniformly distributed over a small sphere of radius a. According to Eq. (1.26) the energy required to assemble the i th point charge is
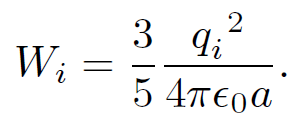 (1.32)
(1.32)
We can think of this as the self-energy of the i th charge. Thus, we can write
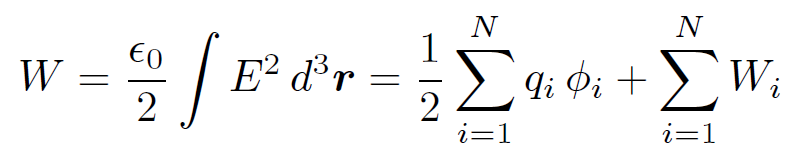 (1.33)
(1.33)
which enables us to reconcile Eqs. (1.10) and (1.19). Unfortunately, if our point charges really are point charges then a → 0 and the self-energy of each charge becomes infinite. Thus, the potential energies predicted by Eqs. (1.10) and (1.19) differ by an infinite amount. What does this all mean? We have to conclude that the idea of locating electrostatic potential energy in the electric field is inconsistent with the assumption of the existence of point charges. One way out of this difficulty would be to say that all elementary charges, such as electrons, are not points but instead small distributions of charge. Alternatively, we could say that our classical theory of electromagnetism breaks down on very small length scales due to quantum effects. Unfortunately, the quantum mechanical version of electromagnetism (quantum electrodynamics or QED, for short) suffers from the same infinities in the self-energies of particles as the classical version. There is a prescription, called renormalization, for steering round these infinities and getting finite answers which agree with experiments to extraordinary accuracy. However, nobody really understands why this prescription works. The problem of the infinite self-energies of charged particles is still unresolved.



|
|
|
|
5 علامات تحذيرية قد تدل على "مشكل خطير" في الكبد
|
|
|
|
|
|
|
لحماية التراث الوطني.. العتبة العباسية تعلن عن ترميم أكثر من 200 وثيقة خلال عام 2024
|
|
|