Electric scalar potential?

We now have a problem. We can only write the electric field in terms of a scalar potential (i.e., E = -∇ϕ) provided that ∇˄E = 0. However, we have just found that in the presence of a changing magnetic field the curl of the electric field is non-zero. In other words, E is not, in general, a conservative field. Does this mean that we have to abandon the concept of electric scalar potential? Fortunately, no. It is still possible to define a scalar potential which is physically meaningful. Let us start from the equation

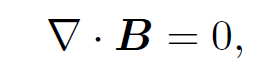 (1.1)

which is valid for both time varying and non-time varying magnetic fields. Since the magnetic field is solenoidal we can write it as the curl of a vector potential:

 (1.2)

So, there is no problem with the vector potential in the presence of time varying fields. Let us substitute Eq. (1.2) into the field

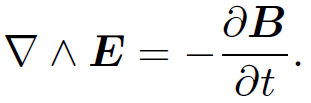
We obtain

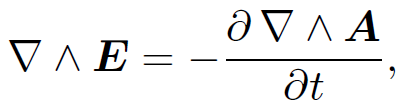 (1.3)

which can be written

 (1.4)

We know that a curl free vector field can always be expressed as the gradient of a scalar potential, so let us write

 (1.5)

or

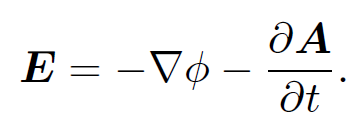 (1.6)

This is a very nice equation! It tells us that the scalar potential ϕ only describes the conservative electric field generated by electric charges. The electric field induced by time varying magnetic fields is non-conservative, and is described by the magnetic vector potential.