
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
Multiplying Vectors
المؤلف:
Professor John W. Norbury
المصدر:
ELEMENTARY MECHANICS & THERMODYNAMICS
الجزء والصفحة:
p 43
12-12-2016
2673
Multiplying Vectors
1. The Scalar Product (often called dot product)
When we add vectors we always get a new vector, namely  When we multiply vectors we get either a scalar or vector. There are two types of vector multiplication called scalar products or vector product. (Sometimes also called dot product or cross product). The scalar product is defined as
When we multiply vectors we get either a scalar or vector. There are two types of vector multiplication called scalar products or vector product. (Sometimes also called dot product or cross product). The scalar product is defined as
 (1.1)
(1.1)
where a and b are the magnitude of 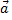 and
and  respectively and ø is the angle between
respectively and ø is the angle between 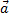 and
and  . The whole quantity
. The whole quantity 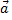 .
.  = ab cos ø is a scalar, i.e. it has magnitude only. Halliday the scalar product is the product of the magnitude of one vector times the component of the other vector along the first vector. Based on our definition (1.1) we can work out the scalar products of all of the unit vectors.
= ab cos ø is a scalar, i.e. it has magnitude only. Halliday the scalar product is the product of the magnitude of one vector times the component of the other vector along the first vector. Based on our definition (1.1) we can work out the scalar products of all of the unit vectors.
Thus we have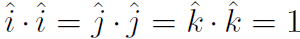 and
and
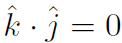 . Now any vector can be written in terms of unit vectors as
. Now any vector can be written in terms of unit vectors as 
 and
and  . Thus the scalar product of any two arbitrary vectors is
. Thus the scalar product of any two arbitrary vectors is

Thus we have a new formula for scalar product, namely
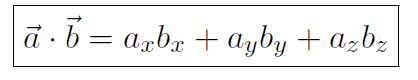 (1.2)
(1.2)
which has been derived from the original definition (1.2)
using unit vectors. What's the good of all this? Well for one thing it's now easy to figure out the angle between vectors, as the next example shows.
2. The Vector Product
In making up the definition of vector product we have to define its magnitude and direction. The symbol for vector product is 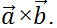 Given that the result is a vector let's write
Given that the result is a vector let's write The magnitude is defined as
The magnitude is defined as

and the direction is defined to follow the right hand rule. (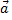 = thumb,
= thumb,  = forefinger,
= forefinger, 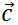 = middle finger.)
= middle finger.)
Thus we have
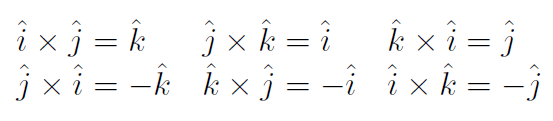
and

Thus the vector product of any two arbitrary vectors is

which gives a new formula for vector product, namely
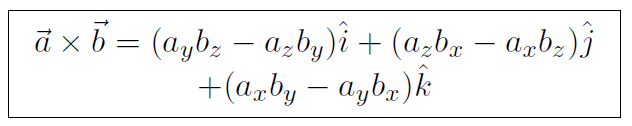
 الاكثر قراءة في الفيزياء العامة
الاكثر قراءة في الفيزياء العامة
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















