


 تاريخ الرياضيات
تاريخ الرياضيات
 الرياضيات في الحضارات المختلفة
الرياضيات في الحضارات المختلفة 
 الرياضيات المتقطعة
الرياضيات المتقطعة
 الجبر
الجبر
 الهندسة
الهندسة 
 المعادلات التفاضلية و التكاملية
المعادلات التفاضلية و التكاملية 
 التحليل
التحليل
 علماء الرياضيات
علماء الرياضيات | LINEAR TIME-OPTIMAL CONTROL-THE MAXIMUM PRINCIPLE FOR LINEAR TIME-OPTIMAL CONTROL |
|
|
|
Read More
Date: 17-10-2016
Date: 9-10-2016
Date: 9-10-2016
|
The really interesting practical issue now is understanding how to compute an optimal control α∗(.).
DEFINITION. We define K(t, x0) to be the reachable set for time t. That is, K(t, x0) = {x1| there exists α(.) ∈ A which steers from x0 to x1at time t}.
Since x(.) solves (ODE), we have x1 ∈ K(t, x0) if and only if
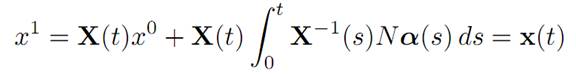
for some control α(.) ∈ A.
THEOREM 1.1 (GEOMETRY OF THE SET K). The set K(t, x0) is convex and closed.
Proof. 1. (Convexity) Let x1, x2 ∈ K(t, x0). Then there exists α1,α2 ∈ A such that
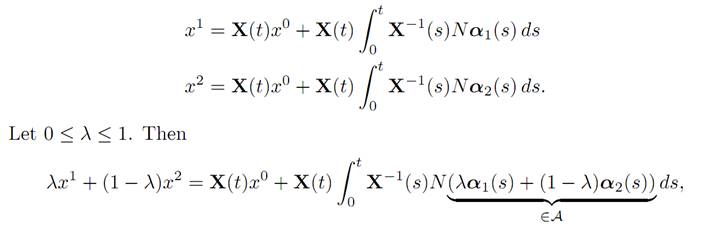
and hence λx1 + (1 − λ)x2 ∈ K(t, x0).
2. (Closedness) Assume xk ∈ K(t, x0) for (k = 1, 2, . . . ) and xk → y. We must show y ∈ K(t, x0). As xk ∈ K(t, x0), there exists αk(.) ∈ A such that
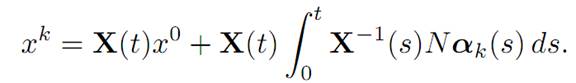
According to Alaoglu’s Theorem, there exist a subsequence kj → ∞ and α ∈ Asuch that αk∗⇀α. Let k = kj → ∞ in the expression above, to find
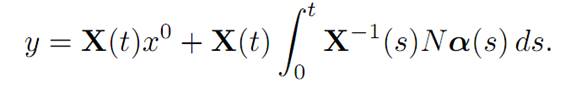
Thus y ∈ K(t, x0), and hence K(t, x0) is closed.
NOTATION. If S is a set, we write ∂S to denote the boundary of S.
Recall that τ∗ denotes the minimum time it takes to steer to 0, using the optimal control α∗. Note that then 0 ∈ ∂K(τ∗, x0).
THEOREM 1.2 (PONTRYAGIN MAXIMUM PRINCIPLE FOR LINEAR TIME-OPTIMAL CONTROL). There exists a nonzero vector h such that
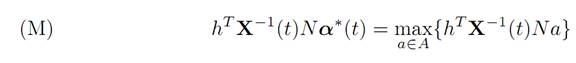
for each time 0 ≤ t ≤ τ∗.
INTERPRETATION. The significance of this assertion is that if we know h then the maximization principle (M) provides us with a formula for computing α∗(.), or at least extracting useful information.
We will see in the next chapter that assertion (M) is a special case of the general Pontryagin Maximum Principle.
Proof. 1. We know 0 ∈ ∂K(τ ∗, x0). Since K( ∗, x0) is convex, there exists a supporting plane to K(τ∗, x0) at 0; this means that for some g = 0, we have
g. x1 ≤ 0 for all x1 ∈ K(τ∗, x0 ).
2. Now x1 ∈ K(τ∗, x0) if and only if there exists α(.) ∈ A such that
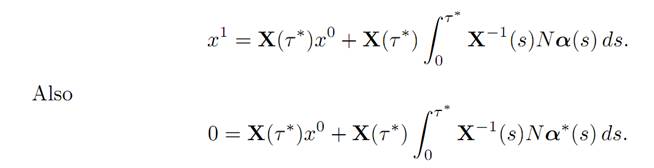
Since g . x1 ≤ 0, we deduce that

for all controls α(.) ∈ A.
3. We claim now that the foregoing implies
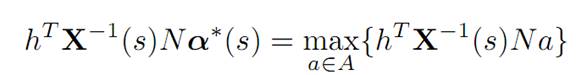
for almost every time s.
For suppose not; then there would exist a subset E ⊂ [0, τ∗] of positive measure, such that
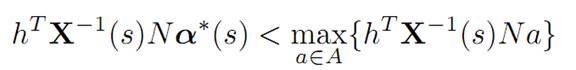
for s ∈ E. Design a new control αˆ (.) as follows:
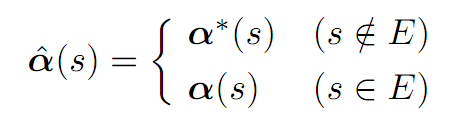
where α(s) is selected so that
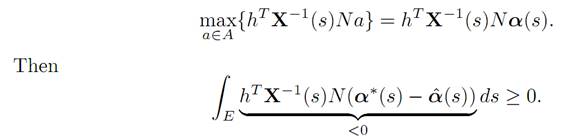
This contradicts Step 2 above.
For later reference, we pause here to rewrite the foregoing into different notation; this will turn out to be a special case of the general theory developed later in Chapter
4. First of all, define the Hamiltonian
H(x, p, a) := (Mx + Na) .p (x, p ∈ Rn, a ∈ A).
THEOREM 1.3 (ANOTHER WAY TO WRITE PONTRYAGIN MAXIMUM PRINCIPLE FOR TIME-OPTIMAL CONTROL). Let α∗(.) be a time
optimal control and x∗(.) the corresponding response.
Then there exists a function p∗(.) : [0, τ∗] → Rn, such that

We call (ADJ) the adjoint equations and (M) the maximization principle. The function p∗(.) is the costate.
Proof. 1. Select the vector h as in Theorem 1.2, and consider the system
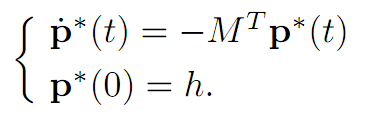
The solution is

and hence

2. We know from condition (M) in Theorem 1.2 that
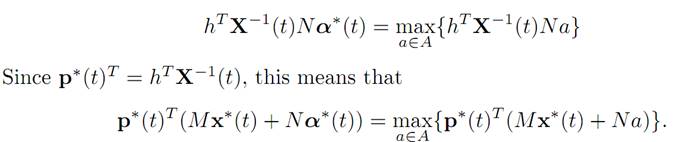
3. Finally, we observe that according to the definition of the Hamiltonian H,
the dynamical equations for x∗(.), p∗(.) take the form (ODE) and (ADJ), as stated in the Theorem.
References
[B-CD] M. Bardi and I. Capuzzo-Dolcetta, Optimal Control and Viscosity Solutions of Hamilton-Jacobi-Bellman Equations, Birkhauser, 1997.
[B-J] N. Barron and R. Jensen, The Pontryagin maximum principle from dynamic programming and viscosity solutions to first-order partial differential equations, Transactions AMS 298 (1986), 635–641.
[C1] F. Clarke, Optimization and Nonsmooth Analysis, Wiley-Interscience, 1983.
[C2] F. Clarke, Methods of Dynamic and Nonsmooth Optimization, CBMS-NSF Regional Conference Series in Applied Mathematics, SIAM, 1989.
[Cr] B. D. Craven, Control and Optimization, Chapman & Hall, 1995.
[E] L. C. Evans, An Introduction to Stochastic Differential Equations, lecture notes avail-able at http://math.berkeley.edu/˜ evans/SDE.course.pdf.
[F-R] W. Fleming and R. Rishel, Deterministic and Stochastic Optimal Control, Springer, 1975.
[F-S] W. Fleming and M. Soner, Controlled Markov Processes and Viscosity Solutions, Springer, 1993.
[H] L. Hocking, Optimal Control: An Introduction to the Theory with Applications, OxfordUniversity Press, 1991.
[I] R. Isaacs, Differential Games: A mathematical theory with applications to warfare and pursuit, control and optimization, Wiley, 1965 (reprinted by Dover in 1999).
[K] G. Knowles, An Introduction to Applied Optimal Control, Academic Press, 1981.
[Kr] N. V. Krylov, Controlled Diffusion Processes, Springer, 1980.
[L-M] E. B. Lee and L. Markus, Foundations of Optimal Control Theory, Wiley, 1967.
[L] J. Lewin, Differential Games: Theory and methods for solving game problems with singular surfaces, Springer, 1994.
[M-S] J. Macki and A. Strauss, Introduction to Optimal Control Theory, Springer, 1982.
[O] B. K. Oksendal, Stochastic Differential Equations: An Introduction with Applications, 4th ed., Springer, 1995.
[O-W] G. Oster and E. O. Wilson, Caste and Ecology in Social Insects, Princeton UniversityPress.
[P-B-G-M] L. S. Pontryagin, V. G. Boltyanski, R. S. Gamkrelidze and E. F. Mishchenko, The Mathematical Theory of Optimal Processes, Interscience, 1962.
[T] William J. Terrell, Some fundamental control theory I: Controllability, observability, and duality, American Math Monthly 106 (1999), 705–719.



|
|
|
|
منها نحت القوام.. ازدياد إقبال الرجال على عمليات التجميل
|
|
|
|
|
|
|
دراسة: الذكاء الاصطناعي يتفوق على البشر في مراقبة القلب
|
|
|
|
|
|
|
هيئة الصحة والتعليم الطبي في العتبة الحسينية تحقق تقدما بارزا في تدريب الكوادر الطبية في العراق
|
|
|