Crystal field theory

   A second approach to the bonding in complexes of the d-block metals is crystal field theory. This is an electrostatic model and simply uses the ligand electrons to create an electric field around the metal center. Ligands are considered as point charges and there are no metal–ligand covalent interactions.

Fig. 1.1 The changes in the energies of the electrons occupying the d orbitals of an M^n‏+ ion when the latter is in an octahedral crystal field. The energy changes are shown in terms of the orbital energies.

The octahedral crystal field

    Consider a first row metal cation surrounded by six ligands placed on the Cartesian axes at the vertices of an octahedron (Figure 1.1a). Each ligand is treated as a negative point charge and there is an electrostatic attraction between the metal ion and ligands. However, there is also a repulsive interaction between electrons in the d orbitals and the ligand point charges. If the electrostatic field (the crystal field) were spherical, then the energies of the five 3d orbitals would be raised (destabilized) by the same amount. However, since the d_z² and d_x²_-y² atomic orbitals point directly at the ligands while the d_xy, d_yz and d_xz atomic orbitals point between them, the d_z² and d_x²_-y² atomic orbitals are destabilized to a greater extent than the d_xy, d_yz and d_xz atomic orbitals (Figure 1.1). Thus, with respect to their energy in a spherical field (the barycentre, a kind of ‘centre of gravity’), the d_z² and d_x²_-y² atomic orbitals are destabilized while the d_xy, d_yz and d_xz atomic orbitals are stabilized. 

   Crystal field theory is an electrostatic model which predicts that the d orbitals in a metal complex are not degenerate. The pattern of splitting of the d orbitals depends on the crystal field, this being determined by the arrangement and type of ligands. It can be deduced that the d_z2 and d_x²_-y² orbitals have eg symmetry, while the d_xy, d_yz and d_xz orbitals possess t₂g symmetry (Figure 1.2). The energy separation between them is Δ_oct (‘delta oct’) or 10Dq. The overall stabi-lization of the t₂g orbitals equals the overall destabilization of the eg set. Thus, orbitals in the eg set are raised by 0.6 Δ_oct with respect to the barycentre while those in the t₂g set are lowered by 0:4Δ_oct. Figure 1.2 also shows these energy differences in terms of 10Dq.

Fig. 1.2 Splitting of the d orbitals in an octahedral crystal field,  with the energy changes measured with respect to the barycentre.

     Both Δ_oct and 10Dq notations are in common use, but we use Δ_oct in this book. The stabilization and destabilization of the t_2g and e_g sets, respectively, are given in terms of Δ_oct . The magnitude of Δ_oct is determined by the strength of the crystal field, the two extremes being called weak field and strong field (equation 1.1).

        (1.1)

  It is a merit of crystal field theory that, in principle at least, values of Δ_oct can be evaluated from electronic spectroscopic data . Consider the d1 complex [Ti)H₂O(₆]³⁺‏, for which the ground state is represented by diagram 1.2 or the notation t₂g 1e_g⁰.

                               (1.2)

  The absorption spectrum of the ion (Figure 1.3) exhibits one broad band for which λ_max = 20300 cm^-1 corresponding to an energy change of 243 kJ mol^-1. (The conversion is 1 cm^-1 = 11.96 ×10^-3 kJ mol^-1.) The absorption results from a change in electronic configuration from t₂g 1eg⁰ to t₂g⁰ eg¹, and the value of λ_max (see Figure 20.15) gives a measure of Δ_oct. For systems with more than one d electron, the evaluation of Δ_oct is more complicated; it is important to remember that Δ_oct is an experimental quantity. Factors governing the magnitude of Δ_oct (Table 1.2) are the identity and oxidation state of the metal ion and the nature of the ligands.   

  We shall see later that Δ parameters are also defined for other ligand arrangements (e.g. Δ_tet).  For octahedral complexes, Δ_oct increases along the following spectrochemical series of ligands; the [NCS]^- ion may coordinate through the N- or S-donor (distinguished in red below) and accordingly, it has two positions in the series:

Fig. 1.3 The electronic spectrum of [Ti(H₂O)₆]³⁺‏ in aqueous solution.

   The spectrochemical series is reasonably general. Ligands with the same donor atoms are close together in the series. If we consider octahedral complexes of d-block metal ions, a number of points arise which can be illustrated by the  following examples:

• the complexes of Cr(III) listed in Table 1.2 illustrate the effects of different ligand field strengths for a given M^n‏+ ion;
• the complexes of Fe(II) and Fe(III) in Table 1.2 illustrate that for a given ligand and a given metal, Δ_oct increases with increasing oxidation state;

Table 1.2 Values of Δ_oct for some d-block metal complexes.

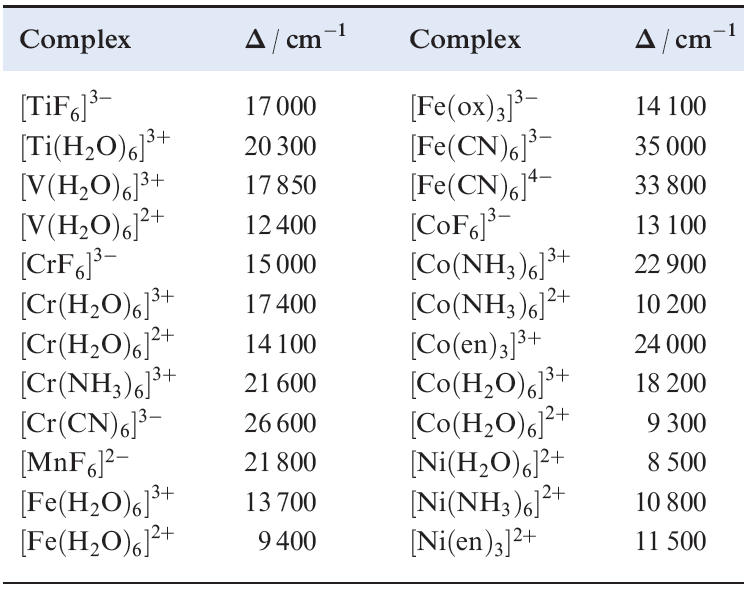
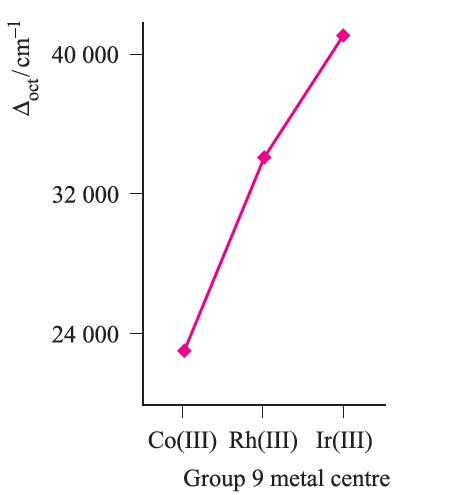
Fig. 1.4 The trend in values of Δ_oct for the complexes [M(NH₃)₆]^3+‏ where M = Co, Rh, Ir.

•  where analogous complexes exist for a series of Mⁿ⁺‏ metals ions (constant n) in a triad, Δ_oct increases significantly down the triad (e.g. Figure 1.4);
•  for a given ligand and a given oxidation state, Δ_oct varies irregularly across the first row of the d-block, e.g. over the range 8000 to 14 000 cm^-1 for the [M)H₂O)₆]^2+‏ ions.

   Trends in values of Δ_oct lead to the conclusion that metal ions can be placed in a spectrochemical series which is independent of the ligands:

Spectrochemical series are empirical generalizations and simple crystal field theory cannot account for the magnitudes of Δ_oct values.