Constant Matrix Perturbation

Consider a system described by a Hamiltonian

(i)

(ii)

(iii)

where and G are positive.

a) Find the eigenvalues and eigenvectors of this Hamiltonian.

b) Consider the two states

(iiii)

(iiiii)

At t = 0, the system is in state |i⟩. Derive the probability that at any later time it is in state |f ⟩.

SOLUTION

a) Define x = ε – λ – G where λ is the eigenvalue. We wish to diagonalize the matrix by finding the determinant of

(1)

(2)

When confronted by a cubic eigenvalue equation, it is best first to try to guess an eigenvalue. The obvious guesses are x = ±G. The one that works is x = -G, so we factor this out to get

(3)

(4)

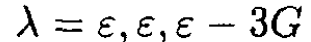(5)

We call these eigenvalues λ₁, λ₂, λ₃, respectively. When we construct the eigenfunctions, only the one for λ₃ is unique. Since the first two have degenerate eigenvalues, their eigenvectors can be constructed in many different ways. One choice is

(6)

(7)

(8)

b) Since the three states ѱ_i form a complete set over this space, we can expand the initial state as

(9)

(10)

(11)

(12)

To find the amplitude in state |f ⟩ we operate on the above equation with ⟨f |. The probability P is found from the absolute-magnitude-squared of this amplitude:

(13)

(14)