


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 15-3-2021
Date: 14-8-2016
Date: 11-8-2016
|
Green’s Reciprocation Theorem
a) Prove Green’s reciprocation theorem: If ϕ is the potential due to a volume charge density ρ within a volume V and a surface charge density σ on the conducting surface S bounding the volume V, while ϕ' is the potential due to another charge distribution ρ' and σ' then

b) A point charge q is placed between two infinite grounded parallel conducting plates. If z0 is the distance between q and the lower plate, find the total charge induced on the upper plate in terms of q, z0, and l, where l is the distance between the plates (see Figure 1.1). Show your method clearly.
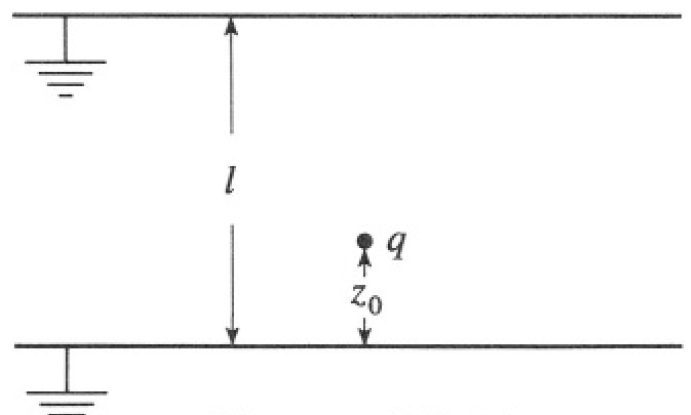
Figure 1.1
SOLUTION
a) We may prove the theorem by considering the volume integral of the following expression:

Integrating by parts in two ways, we have
 (1)
(1)
Now,  (where n points opposite to the directed area of the surface S) and
(where n points opposite to the directed area of the surface S) and 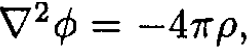 so dividing (1) by 4π yields the desired result:
so dividing (1) by 4π yields the desired result:
 (2)
(2)
b) Let us introduce a second potential given by ϕ' = 2πσ' z, corresponding to a surface charge density on the upper plate of σ' and on the lower plate of 0 (see Figure 1.2). This introduced potential has no charge in the volume, and the real potential is zero on the plates so that the right-hand side of (2) is zero, yielding

where Qi is the induced charge. So on the upper plate,
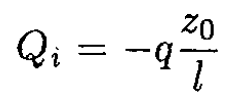
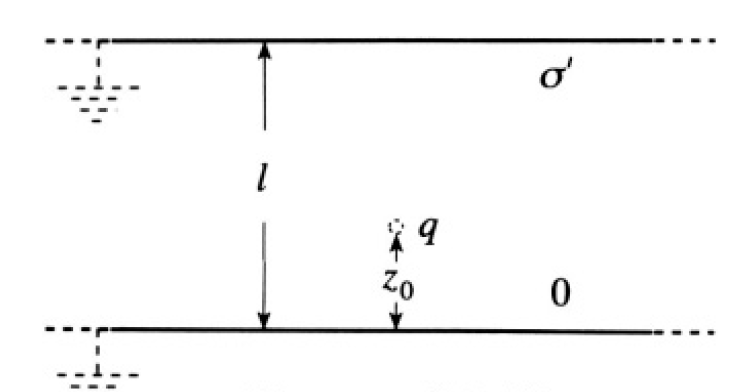
Figure 1.2



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|