Earth-Comet Encounter

Find the maximum time a comet (C) of mass m following a parabolic trajectory around the Sun (S) can spend within the orbit of the Earth (E). Assume that the Earth’s orbit is circular and in the same plane as that of the comet (see Figure 1.1).

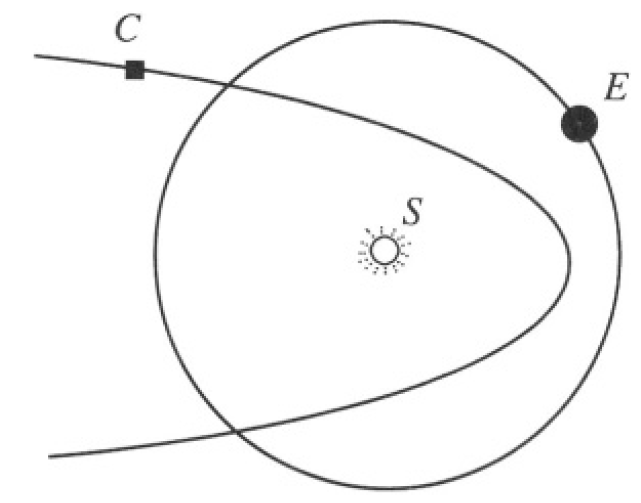
 Figure 1.1

SOLUTION

The total energy of the comet is zero since its trajectory is parabolic. In general,

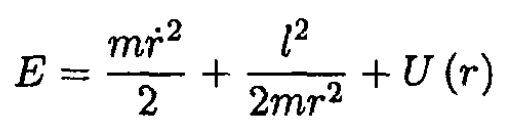(1)

where r is the comet’s distance from the Sun, is its angular momentum, and U(r) is its potential energy (see Figure 1.2). U(r) = -GmM_sun/r,

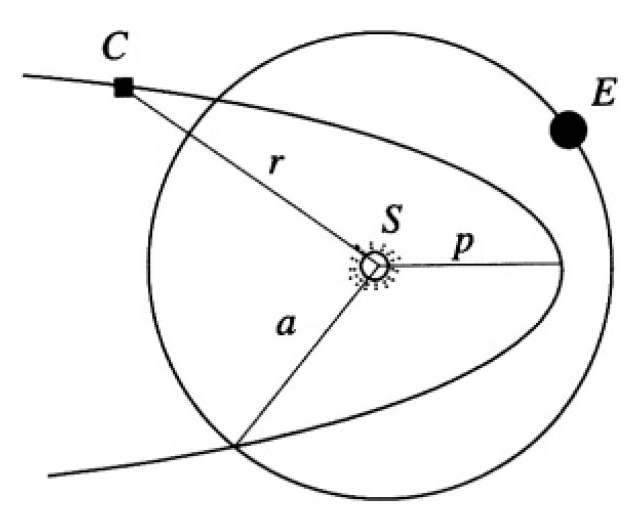
 Figure 1.2

where G is the gravitational constant. Find the total angular momentum defined at the perihelion, where

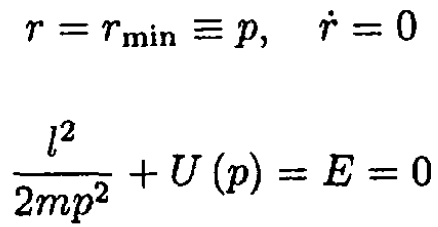
Therefore,

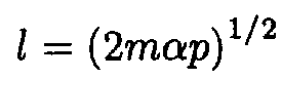(2)

where α = -GmM_sun. From (1)

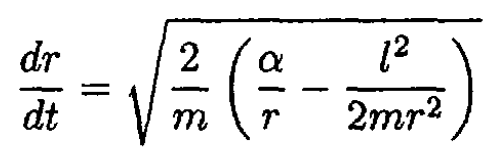
so the time the comet spends inside the Earth’s trajectory is

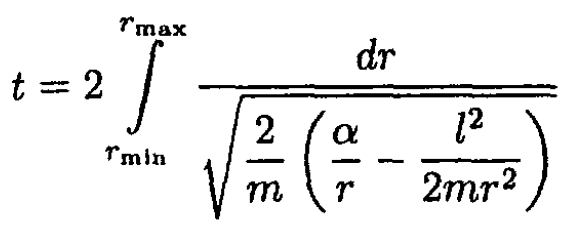
But l² = 2mαp, so from (2)

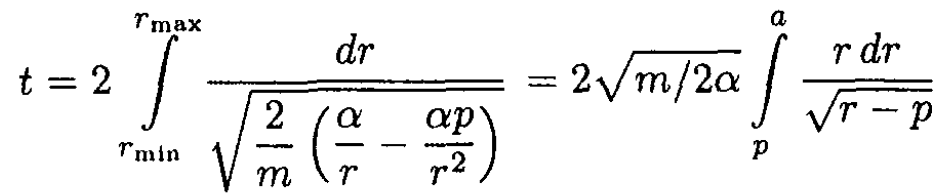 (3)

where a is the radius of the Earth’s orbit. The expression 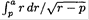 can be easily integrated by parts, yielding

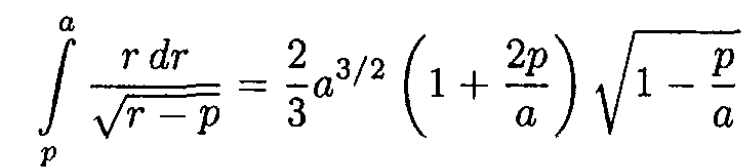
Substituting this result back into (3) gives

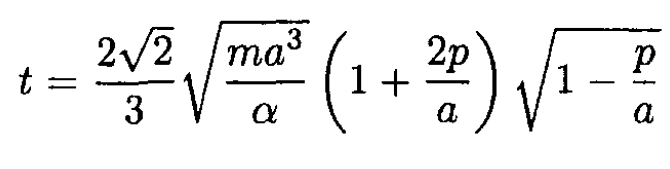
We know that the period of the Earth’s revolution about the Sun equals one year, and noting that 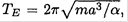 we can rewrite (4) in the form

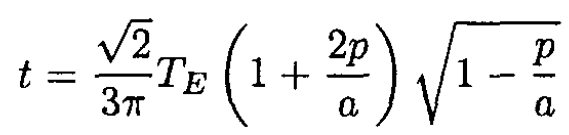
Denoting we find the maximum of 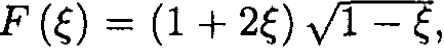  given that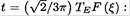

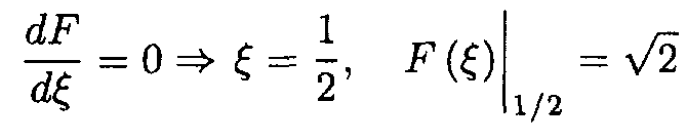
Therefore t_max= 2T_E/3π ≈ 77days = 11 weeks.