


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 11-8-2016
Date: 30-8-2016
Date: 2-8-2016
|
Compton Scattering
In the Compton effect, a γ-ray photon of wavelength λ strikes a free, but initially stationary, electron of mass m. The photon is scattered an angle θ, and its scattered wavelength is 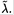 The electron recoils at an angle φ (see Figure 1.1).
The electron recoils at an angle φ (see Figure 1.1).
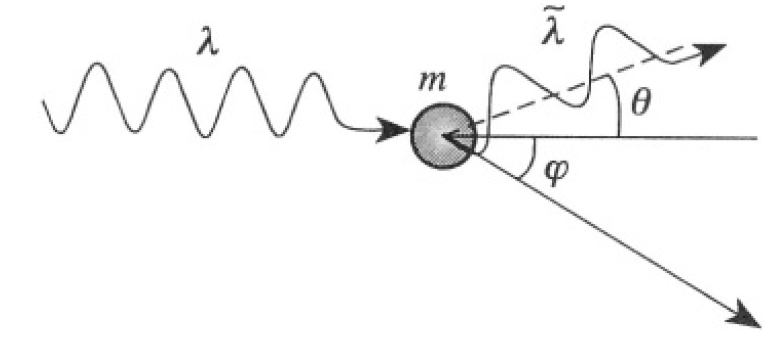
Figure 1.1
a) Write the relativistic equations for momentum and energy conservation.
b) Find an expression for the change  in the photon wavelength for the special case θ = π/2.
in the photon wavelength for the special case θ = π/2.
SOLUTION
a) From momentum and energy conservation we can write
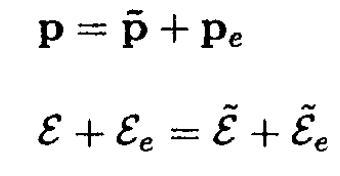 (1)
(1)
where 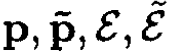 are the momenta and energies of the photon before and after the scattering, respectively,
are the momenta and energies of the photon before and after the scattering, respectively, 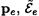 are the final momentum and energies of the electron, and εe is its initial energy. We have for the electron
are the final momentum and energies of the electron, and εe is its initial energy. We have for the electron

and for the photon
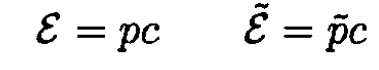
So we can rewrite (1) in the form
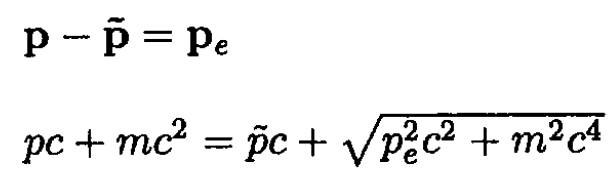 (2)
(2)
b) To solve these equations we can express the momentum of the recoil electron pe in two ways
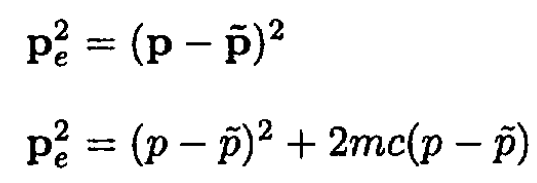 (3)
(3)
from (2).

and for a special case θ = π/2, cosθ = 0. We have
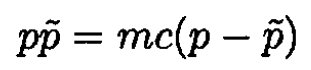
Dividing this equation by  we get
we get

Taking into account that p = h/λ, we obtain the final result:
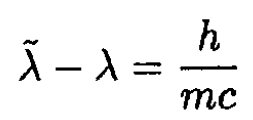



|
|
|
|
التوتر والسرطان.. علماء يحذرون من "صلة خطيرة"
|
|
|
|
|
|
|
مرآة السيارة: مدى دقة عكسها للصورة الصحيحة
|
|
|
|
|
|
|
نحو شراكة وطنية متكاملة.. الأمين العام للعتبة الحسينية يبحث مع وكيل وزارة الخارجية آفاق التعاون المؤسسي
|
|
|