


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
أقرأ أيضاً
التاريخ: 17-2-2016
التاريخ: 15-12-2016
التاريخ: 2023-02-04
التاريخ: 10-8-2017
|
الحركة الجيبية
من الممكن كتابة معادلة رياضية بسيطة لأي جسم يهتز في حركة توافقية بسيطة فالإحداثي x للنقطة p في الشكل 1)) يعطى بالعلاقة :

الشكل (1): عندما يتحرك الجسيم Q على محيط دائرة نصف قطرها x0 بسرعة ثابتة المقدار v0، تتحرك النقطة P حركة توافقية بسيطة من –x0 ≤ x ≤ x0 ، ونظراً لأن نصف قطر الدائرة x0 ، اذن x = x0 cos θ.
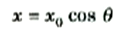
أي أن x تتناسب طريدا مع cos θ , لأن x0 ثابتة. لننظر الآن الى منحني كل من الدالتين sin θ و cos θ كما هو موضحان بالشكل 2)) . هذا الشكل يبين أن كلتي الدالتين تتغيران دوريا من 1- الى 1+ بدورة قدرها ͦͦ360 , أو 2π زاوية نصف قطري. ويتغير cos θ بين هذين الحدين تتغيرx من +x0 الى –x0 ، وهما يمثلان سعة حركتنا التوافقية البسيطة . وهنا تسمى الزاوية θ طورcos θ وsin θ . لا حظ أن المنحنيين متماثلان من جميع

الشكل 2)): منحني الدالة sin θ مقابل θ (الخط الأزرق) والدالة cos θ مقابل θ الزمن (الخط الأخضر).
الوجوه باستثناء أن الدالة sin θ مختلفة عن cos θ بمقدار ربع دورة . ويقال عندئذ ان دالة جيب الزاوية متفاوتة الطور مع دالة جيب تمام الزاوية بمقدار بع دورة، أو 90o.
في وصف الحركة التوافقية البسيطة بالقسم السابق كانت الزاوية θ تتغير مع الزمن بعدد ثابت قدره ω حيث = ωtθ ، وهذا يمكننا من وصف موضع النقطة p في أي لحظة زمنية بالعلاقة:
1)) 
لاحظ أن هذه التعبيرات الثلاثة متكافئة, ومن الحيوي أن تتذكر أن الكمية بين القوسين في هذه التعبيرات الثلاثة مقدرة بالزاوية نصف القطرية. تعرف الحركة التي مكن وصفها كدالة في الزمن على هيئة جيب تماما الزاوية (أو جيب الزاوية) بالحركة الجيبية , أي أن الحركة الجيبية أو الحركة التوافقية البسيطة شيء واحد. ولتخيل الطبيعة الجيبية للحركة التوافقية البسيطة يمكننا الاستعانة بالتجربة المبينة بالشكل (3). ولتخيل الطبيعة الجيبية للحركة التوافقية البسيطة يمكننا الاستعانة بالتجربة التوضيحية المبينة بالشكل3) ). والجهاز المستخدم هنا يتكون من جسم معلق في زنبرك رأسي , وهذا الجسم يحمل قلما يتلامس سنه مع شريط ورقي يتحرك الى اليسار بسرعة ثابتة , فإذا رفع الجسم الى أعلى مسافة قدرها y0 ، فأنه سوف يتحرك حركة توافقية بسيطة سعتها y0، وعندئذ سوف يرسم القلم على الورقة منحني يمثل موضع الجسم اثناء اهتزاز ه الى أعلى والى أسفل.
لنبدأ قياس الزمن ، 0t = ، من لحظة تحرير الجسم , وهذه النقطة هي الطرف الأيسر للمنحني بالجزء (ب) من الشكل. أما موضع الجسم في اللحظة المبينة بالشكل فيحدث بعد مرور زمن معين. ومن ثم يمكن اعتبار هذا المنحني بمثابة رسم بياني لإزاحة الجسم y كدالة في الزمن. وطبقا للمعادلة (1) فإن معادلة هذا المنحني هي:
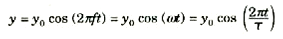

الشكل 3)): ترسم الكتلة المهتزة منحني جيب تمام الزاوية كدالة في الزمن.
وحيث أن a(t) = -(k/m) x(t) في حالة الحركة التوافقية البسيطة , فإن اعتماد a على الزمن يوصف أيضا بنفس الدالة الجيبية , ولكن بإشارة السالبة:
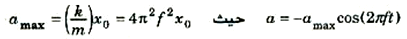



|
|
|
|
"عادة ليلية" قد تكون المفتاح للوقاية من الخرف
|
|
|
|
|
|
|
ممتص الصدمات: طريقة عمله وأهميته وأبرز علامات تلفه
|
|
|
|
|
|
|
المجمع العلمي للقرآن الكريم يقيم جلسة حوارية لطلبة جامعة الكوفة
|
|
|