Expanding Concepts of Fuzzy Set

Example of Fuzzy Set

Example 1.1 Consider a universal set  X which is defined on the age domain.

                                X= {5, 15, 25, 35, 45, 55, 65, 75, 85}

Table 1.1. Example of fuzzy set

We can define fuzzy sets such as “infant”, “young”, “adult” and “senior” in X. The possibilities of each element ofx to be in those four

fuzzy sets are in Table 1.1

We can think of a set that is made up of elements contained in A. This set is called “support” of A.

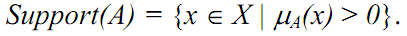
The support of fuzzy set “young” is,

                              Fig. 1.1. Non-Normalized Fuzzy Set and Normalized Fuzzy Set

Support(youth) = {15, 25, 35, 45, 55}

and it is a crisp set. Certainly, the support of “infant” is empty set.

The maximum value of the membership is called “height”. Suppose this “height” of some fuzzy sets is 1, this fuzzy set is “normalized”. The sets

“young”, “adult” and “senior” are normalized (Fig 1.1).

Let’s consider crisp set “teenager”. This crisp set is clearly defined having elements only 10-19 in the universal set X. As you shall notice this

set is a restricted set comparing with X. Similarly fuzzy set “young” is also a restricted set. When we apply a “fuzzy restriction” to universal set X in

certain manner, we get a fuzzy set

1.2 α -Cut Set

Definition ( α -cut set) The  ⍺-cut set  A_⍺ is made up of members whose membership is not less than ⍺.

note that ⍺ is arbitrary. This ⍺-cut set is a crisp set (Fig 1.2).

Example 1.2 The α -cut set is derived from fuzzy set “young” by giving 0.2 to α

this means “the age that we can say youth with possibility not less than 0.2”.

When two cut sets A _α and A_⍺’ exist and if  α ≤ α '  d  for them, then

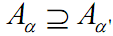
the relation Young_0.2 ⊇ Young_0.8, for example, holds.

                                         Fig. 1.2. α -cut set

Definition (Level set) The value D which explicitly shows the value of the membership function, is in the range of [0,1]. The “level set” is obtained

by the α ’s. That is,

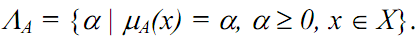
The level set of the above fuzzy set “young” is,

1.3 Convex Fuzzy Set

Definition (Convex fuzzy set) Assuming universal set X is defined in n-dimensional Euclidean Vector space ƒRⁿ 

If all the ⍺- cut sets are convex, the fuzzy set with these α - cut sets is convex(Fig 1.3). In other words, if a

holds, the fuzzy set A is convex.

Fig 1.4 shows a convex fuzzy set and Fig 1.5 describes a non-convex set.

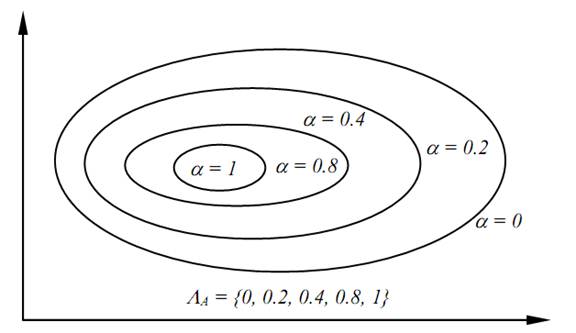
                                              Fig. 1.3. Convex Fuzzy Set

                                                      Fig. 1.4. Convex Fuzzy Set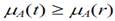

                                                 Fig. 1.5. Non-Convex Fuzzy Set

1.4 Fuzzy Number

“Real number” implies a set containing whole real numbers and “Positive number” implies a set holding numbers excluding negative numbers.

“Positive number less than equal to 10 (including 0)” suggests us a set having numbers from 0 to 10. So

A = “positive number less than equal to 10 (including 0)” = {x | 0 ≤ x ≤ 10, x ∊R }

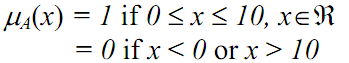
since the crisp boundary is involved, the outcome of membership function is 1 or 0.

Definition (Fuzzy number) If a fuzzy set is convex and normalized, and its membership function is defined in R and  piecewise continuous, it is

called as “fuzzy number”. So fuzzy number (fuzzy set) represents a real number interval whose boundary is fuzzy(Fig 1.6).

1.5 The Magnitude of Fuzzy Set

In order to show the magnitude of fuzzy set, there are three ways of measuring the cardinality of fuzzy set. First, we can derive magnitude by

summing up the membership degrees. It is “scalar cardinality”.

                                           Fig. 1.6. Sets denoting intervals and fuzzy numbers

Following this method, the magnitude of fuzzy set “senior” (in the previous example) is,

|senior| = 0.1 + 0.2 + 0.6 + 1 + 1 = 2.9

Second, comparing the magnitude of fuzzy set A with that of universal set X can be an idea.

This is called “relative cardinality”. In the case of “senior”,

Third method expresses the cardinality as fuzzy set.

Definition (Fuzzy cardinality) Let’s try to get ⍺-cut set (crisp set) A _α , of A. The number of elements is  |A _α |. In other words, the possibility for

number of elements in A to be|A _α | is ⍺. Then the membership degree of fuzzy cardinality |A| is defined as,

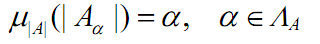
where A _α is a ⍺-cut set and ⩘ _A is a level set.

Example 1.3 If we cut fuzzy set “senior” at α =0.1, there are 5 elements in the α -cut set. senior_0.1 = {45, 55, 65, 75, 85}, |senior_0.1| = 5. In the same

manner, there are 4 elements at α =0.2, there are 3 at α =0.6, there are 2 at α =1. Therefore the fuzzy cardinality of “senior” is

|senior| = {(5, 0.1), (4, 0.2), (3, 0.6), (2,1)}.

1.6 Subset of fuzzy set

Suppose there are two fuzzy setsA andB. When their degrees of membership are same, we say “A and B are equivalent”. That is,

If μ _A(x) ≠ μ _B(x) for any element, then A ≠ B. If the following relation is satisfied in the fuzzy set A and B, A is a subset of B(Fig 1.6).

This relation is expressed as A ⊆ B. We call that A is a subset of B. In addition, if the next relation holds, A is a proper subset of B.

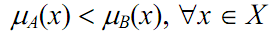
This relation can be written as

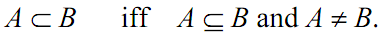
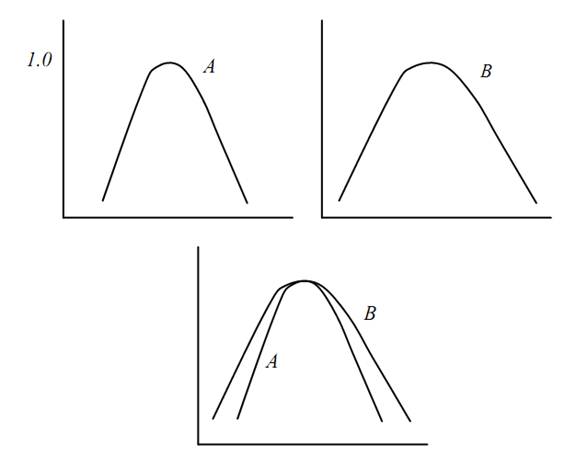
                                                        Fig. 1.6. Subset A ⊂ B

 Kwang H. Lee, First Course on Fuzzy Theory and Applications, 2005, Springer, pag(14-20)

اخر الاخبار

اخبار العتبة العباسية المقدسة

قسم بين الحرمين يقدم ورشة تدريبية عن صيانة العجلات الكهربائية للملاكات الفنية في مدينة الفردوس

مجموعة مشاتل الكفيل تستقبل طلبة مجموعة العميد التربوية

قسم العلاقات العامة ينظم محاضرة ثقافية لوفد مركز الزهراء (عليها السلام) من ألمانيا

المجمع العلمي يحيي ذكرى ولادة الإمام علي (عليه السلام) في كربلاء

المزيد

الآخبار الصحية

طبيب يكشف أفضل مكمل غذائي لتحسين المزاج ودعم الصحة النفسية

دراسة جديدة تكشف أضرار الأطعمة الجاهزة على القلب ؟

6 أطعمة طبيعية تهدئ الزكام دون أدوية.. تعرف عليهم

ماذا يحدث لأعراض الزكام عند تناول الثوم بانتظام؟

المزيد

الآخبار التكنلوجية

ابتكار ثوري في بطاريات السيارات الكهربائية.. سعة أعلى 4 مرات

ماذا يحدث لجسمك عند شرب الماء الساخن يوميا؟

7 فوائد "خفية" لشرب شاي الكركديه كل يوم

دراسة تكشف قدرة الحيتان على سماع الأصوات منخفضة وعالية التردد من مسافة بعيدة

المزيد

مواضيع ذات صلة

THE OPERATION OF FUZZY SET -Standard Operations of Fuzzy Set

FUZZY SETS-Definition of Fuzzy Set

FUZZY SETS-Characteristics of Crisp Set

FUZZY SETS-Operation of Sets

FUZZY SETS-Sets