Sets

1.1 Elements of Sets

An universal set X is defined in the universe of discourse and it includes all possible elements related with the given problem. If we define a set A in

the universal set X, we see the following relationships

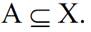
In this case, we say a set A is included in the universal set X. If A is not included in X, this relationship is represented as follows.

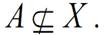
If an elementx is included in the setA, this element is called as a member of the set and the following notation is used.

                                                                                             x ∊ A.

If the elementx is not included in the setA, we use the following notation.

                                                                                           x ∉ A.

In general, we represent a set by enumerating its elements. For example, elements a₁, a₂, a₃,….., a_n are the elements of set A, it is represented as

                                                                                     A = {a₁ , a₂ ,….. , a_n }.

Another representing method of sets is given by specifying the conditions of elements. For example, if the elements of set B should satisfy

the conditions P₁, P₂,….., P_n, then the set B is defined by the following.

                                                                         B = {b | b satisfies p₁, p ₂,…. , p_n }.

In this case the symbol “|” implies the meaning of “such that”.

1.2 Relation between Sets

A set consists of sets is called a family of sets. For example, a family set containing sets A₁, A₂,….is represented by

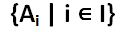
where i is a set identifier and I is an identification set. If all the elements in set A are also elements of set B, A is a subset of B.

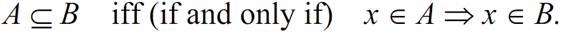
The symbol  ⟹means  “implication”. If the following relation is  satisfied,

                                                 A ⊆ B  and B ⊆A

A andB have the same elements and thus they are the same sets. This relation is denoted by

                                                                    A = B

If the following relations are satisfied between two sets A and B,

                                                                 A Ž⊆ B  and A ≠ B

then B has elements which is not involved in A. In this case, A is called a proper subset of B andthis relation is denoted by

                                                                            A ⊂ B

A set that has no element is called an empty set ⏀‡. An empty set can be a subset of any set.

1.3 Membership

If we use membership function (characteristic function or discrimination function), we can represent whether an element x is involved in a set A or not.

Definition (Membership function) For a set A, we define a membership function 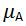maps the elements in the universal set X to the set {0,1}.

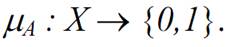
As we know, the number of elements in a setA is denoted by the cardinality |A|. A power set P(A) is a family set containing the subsets of

set A. Therefore the number of elements in the power set P(A) is represented by

|P(A)| = 2^|A| .

Example 1.1 If A = {a, b, c}, then |A| = 3

Kwang H. Lee, First Course on Fuzzy Theory and Applications, 2005, Springer,pag(1-3)