Principles of chromatography

The word “chromatography” means “writing with colour” and refers to the early observations on the separation of dyes by paper chromatography. All chromatographic separations depend upon the differential partition of solutes between two phases, a mobile phase and a stationary phase.  Such partition between two phases is described by the so-called partition coefficient or distribution coefficient.

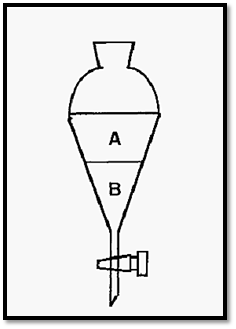
Figure 1. Distribution of a solute between phases in a separating funnel.

Students may  recall  from Chemistry classes how  a dyestuff,  for example, will distribute  itself between two non-miscible liquid phases in a separating funnel.  For any two solvents at a constant  temperature, the distribution coefficient (K_d) is a constant and can be defined as:-

The distribution of a solute is not limited to two liquid phases and the distribution coefficient may describe the  distribution  between  any  two phases, such as liquid/solid or gas/liquid phases.  In  chromatography  there  is  always  a  distribution between two  such  phases,  one  kept  stationary while the other  - the mobile phase  - flows over or through it.  The  stationary  phase can therefore be a solid, a liquid, or a solid coated with  a liquid.  Since it must be fluid, the mobile phase must be either a gas or a liquid.  The mechanism of distribution may not  always be simple partition,  as in a separating funnel.  Examples of the different forms of chromatography are shown in Table 1.

Table 1. Forms of chromatography

In the case  of chromatography,  the  distribution  coefficient  is defined

as:-

Where k is called the partition ratio (or capacity ratio) and fl is the phase ratio.

In chromatography  the  stationary  phase is typically packed into  a tubular column  and the  mobile  phase  flows through  the  packed  column. There is continual equilibration of solutes between the mobile and stationary phases, and that length of column where there  is effectively one equilibration - such as would occur in a separating  funnel - is called a “theoretical plate”. This terminology is derived from fractional distillation of volatile solvents.  Since chromatography  columns are usually vertically  orientated,  the  length  of column  in  which  one equilibration effectively  occurs  is  called  the  “height  equivalent  to  a theoretical plate”,  abbreviated HETP.  The  HETP  is more  of a  concept than a reality, however, because equilibration is actually continuous, not discrete.

The principle of chromatography may be considered by  imagining the column to  consist of a  stack  of theoretical  plates  and,  for  clarity,  the mobile phase may be considered on one  side and the  stationary  phase on the other (Fig. 2).  A column packed  with a bead-form stationary phase (A) may be considered as consisting of a vertical stack  of theoretical plates (B) in each of which an equilibration between the mobile  phase  and the stationary phase takes place.  Subsequent movement of the mobile phase will displace the mobile “half”  of each equilibrated pair downwards, forming new pairs, initially not  in equilibrium, but which will equilibrate before, in turn, being displaced.

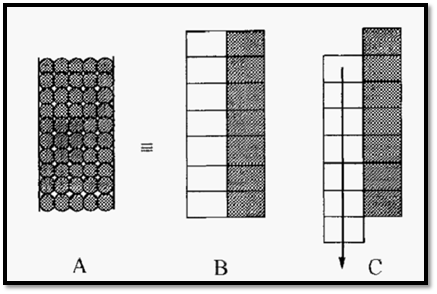
Figure 2. A representation of the mechanism of chromatography.

This representation can be used to  illustrate the  principle of chromatography, as in the tutorial exercise shown in Fig. 3.

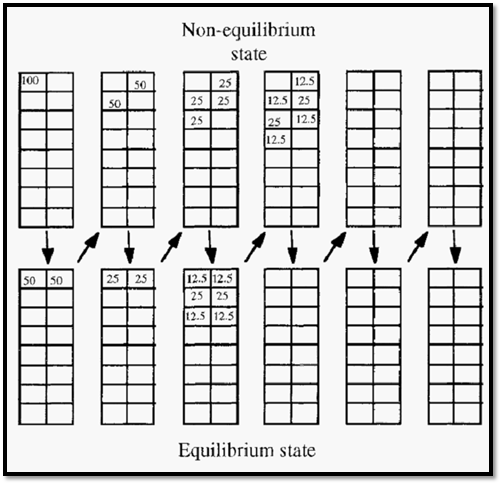
Figure 3.  A tutorial illustrating the principle of chromatography.

One hundred units of solute arc injected into the mobile phase of the column (Fig. 3, top  left).  This then equilibrates with the  stationary phase (bottom  left) - assume a partition ratio of 1  in this case.

Movement of the mobile phase carries the  solute downwards to a new area of the  column (top,  second from  left),  where equilibrium again occurs (bottom,  second from  left).  To  see  if you have  grasped the concept. try to fill in the  remainder of the numbers, until the  right hand columns are filled in. Note the movement of the “peak”, relative to the mobile phase, and note how the peak spreads out.

Figure 4. Illustration of retention time (T,) and peak width (W).

The number of theoretical plates (N) in a column is given by the equation:-

Where

 Tr = retention time

W = peak width, measured as shown in Fig. 4.

a = a method-dependent constant.

Dividing the  length  of the  packed column bed by the  number of theoretical plates gives the HETP.  Note that the larger the value of N, the smaller the HETP value and the more efficient the column.  For a given retention  time, equation  .1  indicates that  an efficient  column (where N  is large)  will give  peaks  of smaller width than  an  inefficient column.

---------------------------------------------------------------------------------------

Resolution of peaks.

The resolution (R), which describes how well any two peaks are separated, is described by the equation:-

From this it will be seen that the narrower the  peak  (i.e. the  higher

the value of N), the better the resolution will be.

-----------------------------------------------------------------------------------------

The magnitude  of the  HETP,  which should be as small as possible, is influenced by:

•  the particle  size  of the  stationary  phase, and,

•  the flow rate of the mobile phase.

1. The effect of particle size

Reconsider the  equilibration  of  a  solute  between  two  phases  in  a separating funnel.  How quickly equilibrium is achieved will depend upon:-

•  diffusion across the boundary  between A and B, which is proportional

to the  surface area of the boundary, and,

• diffusion  within A and B to  the  boundary;  the  time  taken  depending upon the distance from the boundary.

For a minimal time  to  equilibrium, therefore,  the  boundary surface area should be maximized and the distance of any part of the  solutions, A and B, from the boundary should be minimized.  This could be achieved by using a separating funnel of unusual design as shown in Fig. 5.

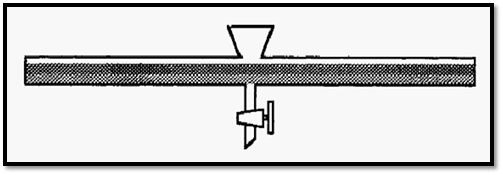
Figure 5. A hypothetical separating funnel for rapid equilibration.

However, the more conventional  way of speeding up the  attainment of equilibrium  is by shaking  the  separating  funnel,  so  that  the  solutions are well mixed.  The two  phases  remain  separate  but one  solution  will be dispersed in the other, usually in the form of small spheres.

The volume of a single sphere is given by:-

If the total volume of the dispersed phase is “V”,  then  V will be dispersed into “N”  spheres, where:-

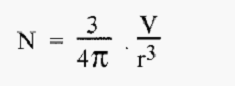
i.e. the number of spheres is inversely proportional to r³.

The surface area of a single sphere is given by:-

Therefore, surface area of N  spheres

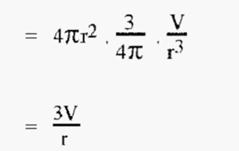
i.e. as the radius of the spheres “r”  gets smaller, the total surface area gets larger.

Since the  surface  area constitutes  the  interface  between the  phases,  a small value of “r” will ensure a maximal interface area and rapid equilibration. Also, in a sphere, the greatest distance that a solute molecule can  be  from  the  surface  is  “r”,  the  radius  of  the  sphere.

Therefore, to minimize the diffusion distance and the time to  equilibrium, “r” should be minimal. The largest possible distance to the surface for a molecule outside of the packing material also decreases as r  decreases.

Shaking a separating  funnel  vigorously  is an  effective  way of making small spheres and hence of rapidly equilibrating the phases.  Similarly, for rapid equilibration, the best size for the  spherical  particles  of a chromatography resin is “as small as possible”. For even packing and good flow characteristics,  the  resin  particles  should also  be of uniform size.

As “r” decreases, however, the total surface area increases and so the resistance to the flow of the mobile phase also increases.  Very small particles, therefore, dictate the use of high pressure pumps - hence HPLC (high pressure liquid chromatography).

2. The effect of the mobile phase flow rate

The effect of the flow rate of the mobile phase is expressed by the  so-called Van Deemter equation:-

Where,

HETP = height equivalent to a theoretical plate

F = mobile phase flow rate

A = eddy diffusion (independent of F)

B= molecular diffusion (increases as F decreases)

C  =  resistance to mass transfer (i.e. smearing) (increases as F increases)

An “eddy” is a swirl in a liquid. “Eddy” diffusion refers to the fact that the mobile phase has to follow a tortuous path  around the  resin particles, inevitably resulting in some mixing and consequent dilution of a solute peak.

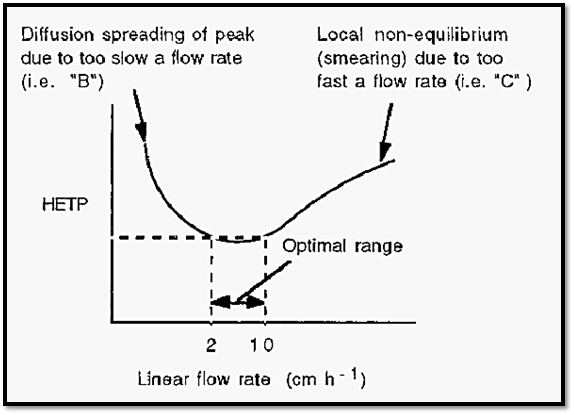
Figure 6. A schematic plot of the van Deemter equation.

If there was no flow in the column, the  solute peak would spread with time due to diffusion of the solute molecules, from an area where they are in high concentration  to  an  area where their  concentration  is less. Similarly, when the flow  rate  is too  slow, the  peak  will have  ample  time to spread due to diffusion.  On the  other  hand,  if the  flow is too  fast, solute molecules in the  mobile phase will pass the  stationary  phase without properly equilibrating with it,  resulting in  peak  broadening  due to “smearing”. The optimal linear flow rate for typical low-pressure, molecular exclusion chromatography lies in the range  of 2-10 cm h^-1.

2.1 The relationship between linear and volumetric flow rates.

The easiest way of measuring the  mobile phase flow rate  is to  collect the effluent stream  in a measuring cylinder and measure the  amount collected in a given time interval.  The result will be the  volumetric flow rate, which can be expressed in ml h^-1. For the chromatographic process, however, the  important  point  is not the volumetric flow rate  per se  but how fast the mobile phase flows past the stationary phase.

A moment is  reflection  will reveal that  a given  volumetric  flow  rate will give very  different  chromatographic  conditions  in  a  thin  column compared to  a fat  column  as the  mobile phase  will flow past the stationary phase faster in the thin column than in the fat column.  To make the  chromatographic  conditions  the  same  in columns of any diameter, the flow rate can be expressed as the linear flow rate,  with units of cm  h^-1.

The relationship between the volumetric and linear flow rates  is given by the equation:-

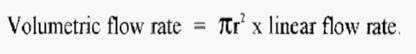
As an  example  of the  utility  of the  concept  of linear  flow  rate, imagine that  you have developed a successful chromatographic separation, using a column of 2.5 cm i.d. and a volumetric flow rate of 50ml h^-1.  You then move to another lab to apply your separation method, as a temporary visitor, but you find that the new lab only has columns of 2.0 cm i.d.  What can you do about this?

First calculate the length  ℓ  that  50  ml would occupy  in  the  2.5 cm column:-

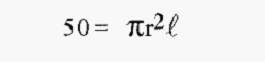
The linear flow rate in the  2.5 cm i.d. column is thus  10.186  cm h^-1. From this, calculate the Volumetric flow (“x”) in the 2.0 cm i.d. column that would give the same linear flow rate, i.e.;-

And for

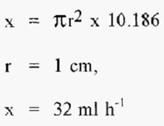
Thus the required volumetric flow rate in the 2.0 cm column is 32 cm h^-1. The 2.0 cm i.d. column could be operated at the same length as the 2.5 cm i.d. column, but at the reduced volumetric flow rate of 32 cm h^-1.

References

-Dennison, C. (2002). A guide to protein isolation . School of Molecular mid Cellular Biosciences, University of Natal . Kluwer Academic Publishers new york, Boston, Dordrecht, London, Moscow .