


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 7-3-2016
Date: 7-3-2016
Date: 26-10-2020
|
CAVITY RADIATION AND CAVITY MODES
To derive a mathematical expression to describe the blackbody radiation curve, many approaches were taken. As it is difficult to compute the behavior of a real blackbody, an easier avenue was found by Wein in the form of a cavity radiator, in which we assume that the object is a heated (isothermal) cavity with a hole in it from which light is emitted. Inside the enclosure the absorption of energy balances with emission. The cavity itself may be seen as a resonator in which standing waves are present. To simplify the problem further (to permit mathematical analysis), consider a cubical heated cavity of dimensions L (Figure 1.1). A standing wave can be produced in any one of three dimensions, and standing waves of various wavelengths are possible as long as they fit inside the cavity (i.e., are an integral multiple of the dimensions of the cavity). The condition exists, then, that any electromagnetic wave (e.g., a light wave) inside the cavity must have a node at the walls of the cavity. As frequency increases, more nodes will fit inside the cavity, as evident in Figure 1.1. Rayleigh and Jeans showed mathematically that the number of modes per unit frequency per unit volume in such a cavity is
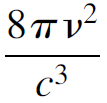 (1.1)
(1.1)
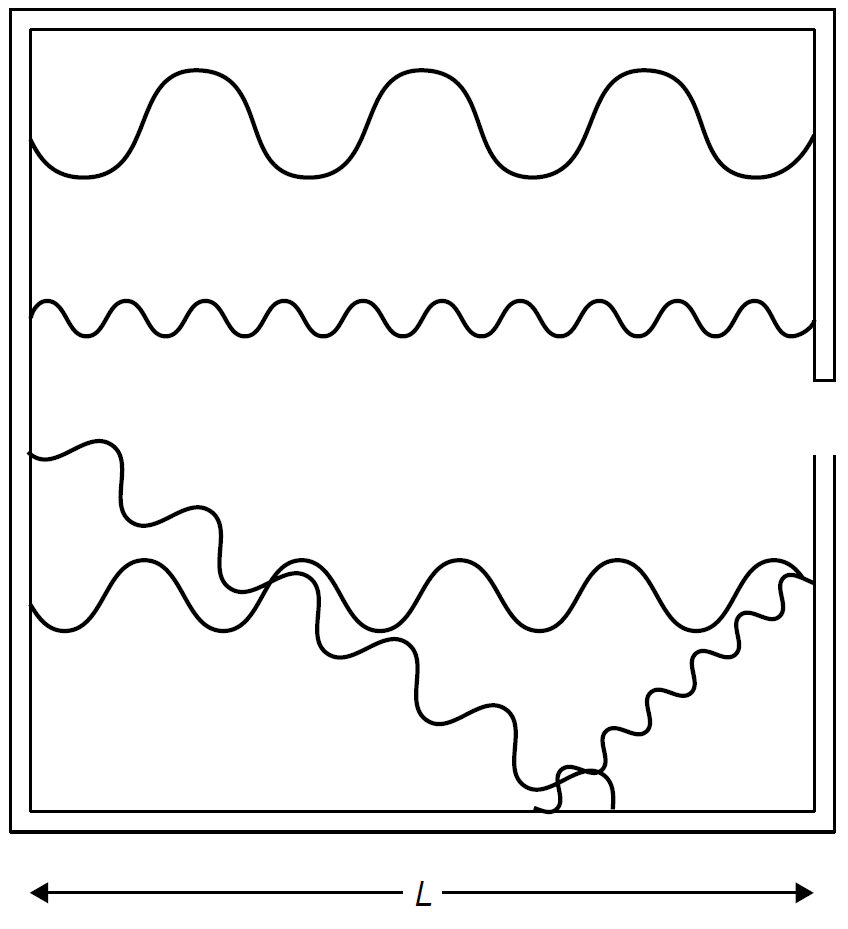
Figure 1.1. Modes in a heated cavity.
where v is the frequency of the mode and c is the speed of light. Rayleigh and Jeans went on to postulate that the probability of occupying any given mode is equal for all modes (in other words, all wavelengths are radiated with equal probability), an assumption from classical wave theory, and that the average energy per mode was kT (from Boltzmann statistics). The last assumption was made according to the classical pre quantum (i.e., before the Rutherford atomic model) view of radiation, in which each atom with an orbiting electron was considered to be an oscillator continually emitting radiation with an average energy of kT. The resulting law formulated by Rayleigh and Jeans describes the intensity of a blackbody radiator as a function of temperature as follows:
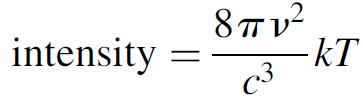 (1.2)
(1.2)
The law works well at low frequencies (i.e., long wavelengths); however, at higher frequencies it predicts an intense ultraviolet (UV) output, which simply was not observed. For any given object, 16 times as much energy observed as red light should be emitted as violet light, and this simply does not happen. This law predicts the equilibrium intensity to be proportional to kTv2, a result that may be arrived at using classical electromagnetic theory and which states that an oscillator will radiate energy at a rate proportional to v2. This failure of the Rayleigh Jeans law, dubbed the UV catastrophe, illustrates the problems with applying classical physics to the domain of light and why a new approach was needed. A different approach to the problem was developed by Max Planck in 1899. His key assumption was that the energy of any oscillator at a frequency v could exist only in discrete (quantized) units of hv, where h was a constant (called Planck’s constant). The fundamental difference in this approach from the classical approach was that modes were quantized and required an energy of hv to excite them (more on this in the next section). Upper modes, with higher energies, were hence less likely to be occupied than lower-energy modes. Bose Einstein statistics predict the average energy per mode to be the energy of the mode times the probability of that mode being occupied. Central to this idea was that the energy of the actual wave itself is quantized as E = hv. This is not a trivial result and is examined, where experimental proof of this relation will be given. Multiplying this energy by the probability of a mode being occupied (the Bose Einstein distribution function) gives the average energy per mode as
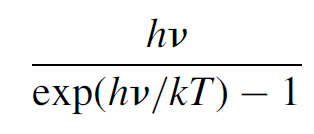 (1.3)
(1.3)
where h is Planck’s constant, v the frequency of the wave, k is Boltzmann’s constant, and T is the temperature. When this is multiplied by the number of modes per unit frequency per unit volume, the same number that Rayleigh and Jeans computed, the resulting formula allows calculation of the intensity radiated at any given wavelength for any given temperature:
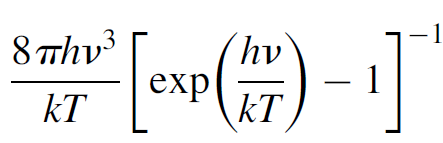 (1.4)
(1.4)
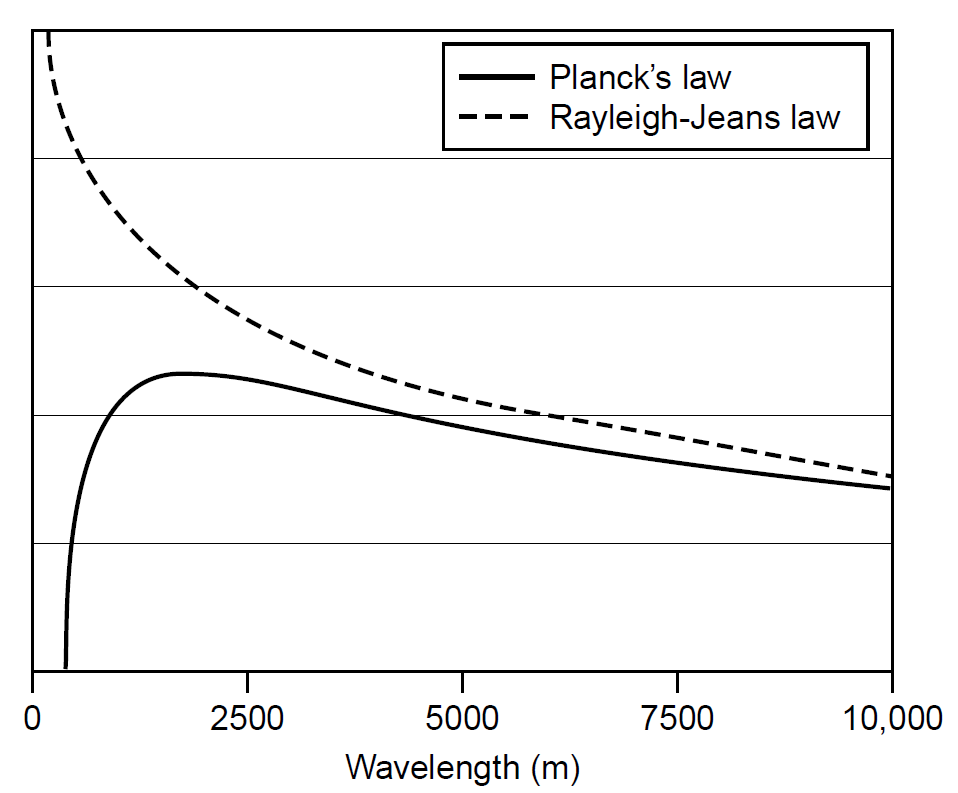
Figure 1.2. UV catastrophe and Planck’s law.
Comparing Planck’s radiation formula to the classical Rayleigh Jeans law, we see that the two results agree well at low frequencies but deviate sharply at higher frequencies, with the Rayleigh Jeans law predicting the UV catastrophe that never occurred (Figure 1.2). This new approach, which fit experimentally obtained data, heralded the birth of quantum mechanics,



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|