


 الفيزياء الكلاسيكية
الفيزياء الكلاسيكية
 الكهربائية والمغناطيسية
الكهربائية والمغناطيسية
 علم البصريات
علم البصريات
 الفيزياء الحديثة
الفيزياء الحديثة
 النظرية النسبية
النظرية النسبية
 الفيزياء النووية
الفيزياء النووية
 فيزياء الحالة الصلبة
فيزياء الحالة الصلبة
 الليزر
الليزر
 علم الفلك
علم الفلك
 المجموعة الشمسية
المجموعة الشمسية
 الطاقة البديلة
الطاقة البديلة
 الفيزياء والعلوم الأخرى
الفيزياء والعلوم الأخرى
 مواضيع عامة في الفيزياء
مواضيع عامة في الفيزياء|
Read More
Date: 26-1-2017
Date: 29-1-2017
Date: 29-1-2017
|
Entropy of the Free Quantum Field in Rindler Space
In the real world, a wide variety of different phenomena take place at different temperature scales. At the lowest temperatures where only massless quanta are produced by thermal fluctuations, one expects to find a very weakly interacting gas of gravitons, photons, and neutrinos. Increase the temperature to the e+, e− threshold and electron-positron pairs are produced. The free gas is replaced by a plasma. At higher temperatures, pions are produced which eventually dissociate into quarks and gluons, and so it goes, up the scale of energies. Finally, the Planck temperature is reached where totally new phenomena of an as yet unimagined kind take place.
All of these phenomena have their place in the Fido's description of the region near a horizon. In this lecture we will consider an enormously oversimplified description of the world in which only a single free field is present in a fixed space-time background. There is serious danger in extrapolating far reaching conclusions from so oversimplified a situation. In fact, the paradoxes and contradictions associated with black holes, quantum mechanics, and statistical thermodynamics that these lectures are concerned with are largely a consequence of such unjustified extrapolation. Nevertheless, the study of a free quantum field in Rindler space is a useful starting point.
Fourier decomposing the field χ leads to the wave equation.
 (1.1)
(1.1)
In order to quantize the field χ it is necessary to provide a boundary condition when u→ −∞. The simplest method of dealing with this region is to introduce a cutoff at some point uo = log ϵ at which point the field (or its first derivative) is made to vanish. The parameter ϵ represents the proper distance of the cutoff point to the horizon. Physically we are introducing a perfectly reflecting mirror just outside the horizon at a distance ϵ.Later we will remove the cutoff by allowing uo →−∞.
It is by no means obvious that a reflecting boundary condition very near the horizon is a physically reasonable way to regularize the theory. However it will prove interesting to separate physical quantities into those which are sensitive to ϵ and those which are not. Those things which depend on ϵ are sensitive to the behavior of the physical theory at temperatures of order 1/2π3 and greater.
Each transverse Fourier mode χk can be thought of as a free 1+1 dimensional quantum field confined to a box. One end of the box is at the reflecting boundary at u = uo = log ϵ. The other wall of the box is provided by the repulsive potential
V (u) = k2 exp(2u)
which becomes large when u > −log k. Thus we may approximate the potential by a second wall at u = u1 = −log k. The total length of the box depends on k and ϵ according to
L(k) = −log(ϵ k) (1.2)
For each value of k the field χk can be expanded in mode functions and creation and annihilation operators according to
 (1.3)
(1.3)
where the mode (n, k) has frequency λ(n, k).The Rindler Hamiltonian is given by
 (1.4)
(1.4)
where
 (1.5)
(1.5)
Thus far the quantization rules are quite conventional. The new and unusual feature of Rindler quantization, is that we do not identifiy the vacuum with the state annihilated by the a(n, k), but rather with the thermal density matrix
 ( 1.6)
( 1.6)
with
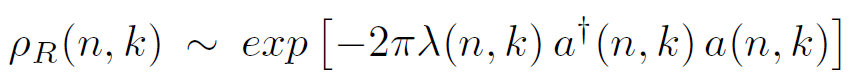 (1.7)
(1.7)
Thus the average occupation number of each mode is
 (1.8)
(1.8)
These particles constitute the thermal atmosphere.
The reader might wonder what goes wrong if we choose the state which is annihilated by the a's. Such a state is not at all invariant under translations of the original Minkowski coordinates Z and T .In fact, a careful computation of the expectation value of T μν in this state reveals a singular behavior at the horizon. Certainly this is not a good candidate to represent the original Minkowski vacuum.
A black hole, on the other hand, is not a translationally invariant system. One might therefore suppose that the evolution of the horizon might lead to the Fock space vacuum with no quanta rather than the thermal state. This however would clearly violate the fourth guiding principle stated in the introduction: To a freely falling observer, the horizon of a black hole should in no way appear special. Moreover, the large back reaction on the gravitational field that would result from the divergent expectation value of T μν makes it unlikely that this state can exist altogether.
Physical quantities in Rindler space can be divided into those which are sensitive to the cutoff at ϵ and those which are not. As an example of insensitive quantities, the field correlation functions such as
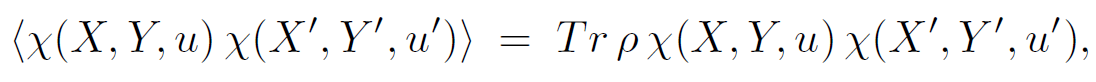 (1.9)
(1.9)
are found to have smooth limits as ϵ → 0, as long as the points (X, Y, u) and (X', Y ', u' ) are kept away from the horizon. Therefore such quantities can be said to decouple from the degrees of freedom within a distance ϵ of the horizon. A much more singular quantity which will be of great concern in future lectures is the entropy of the vacuum state. Since the relevant density matrix has the Maxwell–Boltzmann. Defining
 (1.10)
(1.10)
and using the identity
 (1.11)
(1.11)
we obtain
 (1.12)
(1.12)
Defining E = <H> and F = −1/β logZ we find the usual thermodynamic identity
S = β(E − F) (1.13)
Another identity follows from using E = −∂logZ /∂β where we find
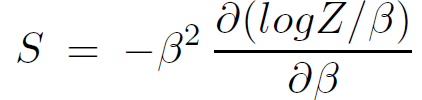 (1.14)
(1.14)
The entropy S in equations 1.13 and 1.14 can be thought of as both entanglement and thermal entropy in the special case of the Rindler space density matrix. This is because the effect of integrating over the fields χL is to produce the thermal density matrix. Thus the computation of the entropy of Rindler space is reduced to ordinary thermodynamic methods. For the present case of free fields the entropy is additive over the modes and can be estimated from the formula for the thermodynamics of a free 1+1 dimensional scalar field.
To compute the total entropy we begin by replacing the infinite transverse X, Y plane by a finite torus with periodic boundary conditions. This has the effect of discretizing the values of k. Thus
 (1.15)
(1.15)
where B is the size of the torus.
The entropy stored in the field χk can be estimated from the entropy density of a 1+1 dimensional massless free boson at temperature T. A standard calculation gives the entropy density S/L to be given by
 (1.16)
(1.16)
where T is the temperature. Substituting T = 1/2π and equation 1.2 for the length L gives the entropy of χk
 (1.17)
(1.17)
To sum over the values of k we use equation 1.15 and let B →∞
 (1.18)
(1.18)
In evaluating equation 1.18, the integral must be cut off when k > 1/ϵ . This is because when k = 1/ϵ the potential is already large at u = uo so that the entire contribution of χk is supressed. We find that S is approximately
 (1.19)
(1.19)
From equation 1.19 we see two important features of the entropy of Rindler space. The first is that it is proportional to the transverse area of the horizon, B2.One might have expected it to diverge as the volume of space, but this is not the case. The entropy is stored in the vicinity of the stretched horizon and therefore grows only like the area. The second feature which should alarm us is that the entropy per unit area diverges like 1/ϵ2 .As we shall see, the entropy density of the horizon is a physical quantity whose exact value is known. Nevertheless the divergence in S indicates that its value is sensitive to the ultraviolet physics at very small length scales.
Further insight into the form of the entropy can be gained by recalling that the proper temperature T (ρ) is given by T (ρ) = 1/2πρ. Furthermore the entropy density of a 3+1 dimensional free scalar field is given by
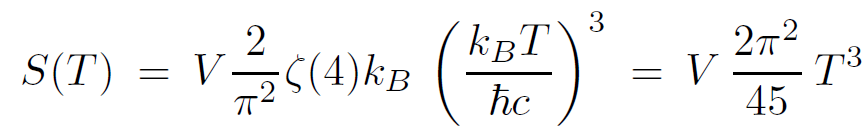 (1.20)
(1.20)
Now consider the entropy stored in a layer of thickness δρ and area B2 at
a distance ρ from the horizon
 (1.21)
(1.21)
To find the full entropy we integrate with respect to ρ
 (1.22)
(1.22)
Now we see that the entropy is mainly found near the horizon because that is where the temperature gets large.



|
|
|
|
دراسة يابانية لتقليل مخاطر أمراض المواليد منخفضي الوزن
|
|
|
|
|
|
|
اكتشاف أكبر مرجان في العالم قبالة سواحل جزر سليمان
|
|
|
|
|
|
|
اتحاد كليات الطب الملكية البريطانية يشيد بالمستوى العلمي لطلبة جامعة العميد وبيئتها التعليمية
|
|
|