
تاريخ الفيزياء

علماء الفيزياء


الفيزياء الكلاسيكية

الميكانيك

الديناميكا الحرارية


الكهربائية والمغناطيسية

الكهربائية

المغناطيسية

الكهرومغناطيسية


علم البصريات

تاريخ علم البصريات

الضوء

مواضيع عامة في علم البصريات

الصوت


الفيزياء الحديثة


النظرية النسبية

النظرية النسبية الخاصة

النظرية النسبية العامة

مواضيع عامة في النظرية النسبية

ميكانيكا الكم

الفيزياء الذرية

الفيزياء الجزيئية


الفيزياء النووية

مواضيع عامة في الفيزياء النووية

النشاط الاشعاعي


فيزياء الحالة الصلبة

الموصلات

أشباه الموصلات

العوازل

مواضيع عامة في الفيزياء الصلبة

فيزياء الجوامد


الليزر

أنواع الليزر

بعض تطبيقات الليزر

مواضيع عامة في الليزر


علم الفلك

تاريخ وعلماء علم الفلك

الثقوب السوداء


المجموعة الشمسية

الشمس

كوكب عطارد

كوكب الزهرة

كوكب الأرض

كوكب المريخ

كوكب المشتري

كوكب زحل

كوكب أورانوس

كوكب نبتون

كوكب بلوتو

القمر

كواكب ومواضيع اخرى

مواضيع عامة في علم الفلك

النجوم

البلازما

الألكترونيات

خواص المادة


الطاقة البديلة

الطاقة الشمسية

مواضيع عامة في الطاقة البديلة

المد والجزر

فيزياء الجسيمات


الفيزياء والعلوم الأخرى

الفيزياء الكيميائية

الفيزياء الرياضية

الفيزياء الحيوية

الفيزياء العامة


مواضيع عامة في الفيزياء

تجارب فيزيائية

مصطلحات وتعاريف فيزيائية

وحدات القياس الفيزيائية

طرائف الفيزياء

مواضيع اخرى
An experiment with bullets
المؤلف:
Richard Feynman, Robert Leighton and Matthew Sands
المصدر:
The Feynman Lectures on Physics
الجزء والصفحة:
Volume I, Chapter 37
2024-04-17
1621
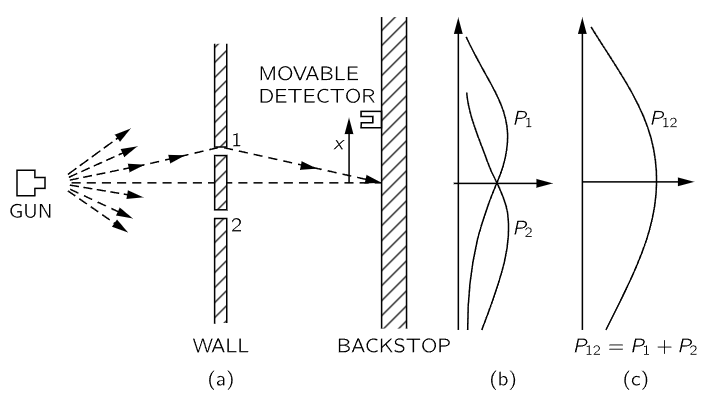
Fig. 37–1. Interference experiment with bullets.
To try to understand the quantum behavior of electrons, we shall compare and contrast their behavior, in a particular experimental setup, with the more familiar behavior of particles like bullets, and with the behavior of waves like water waves. We consider first the behavior of bullets in the experimental setup shown diagrammatically in Fig. 37–1. We have a machine gun that shoots a stream of bullets. It is not a very good gun, in that it sprays the bullets (randomly) over a fairly large angular spread, as indicated in the figure. In front of the gun, we have a wall (made of armor plate) that has in it two holes just about big enough to let a bullet through. Beyond the wall is a backstop (say a thick wall of wood) which will “absorb” the bullets when they hit it. In front of the backstop, we have an object which we shall call a “detector” of bullets. It might be a box containing sand. Any bullet that enters the detector will be stopped and accumulated. When we wish, we can empty the box and count the number of bullets that have been caught. The detector can be moved back and forth (in what we will call the x-direction). With this apparatus, we can find out experimentally the answer to the question: “What is the probability that a bullet which passes through the holes in the wall will arrive at the backstop at the distance x from the center?” First, you should realize that we should talk about probability, because we cannot say definitely where any particular bullet will go. A bullet which happens to hit one of the holes may bounce off the edges of the hole, and may end up anywhere at all. By “probability” we mean the chance that the bullet will arrive at the detector, which we can measure by counting the number which arrive at the detector in a certain time and then taking the ratio of this number to the total number that hit the backstop during that time. Or, if we assume that the gun always shoots at the same rate during the measurements, the probability we want is just proportional to the number that reach the detector in some standard time interval.
For our present purposes we would like to imagine a somewhat idealized experiment in which the bullets are not real bullets, but are indestructible bullets—they cannot break in half. In our experiment we find that bullets always arrive in lumps, and when we find something in the detector, it is always one whole bullet. If the rate at which the machine gun fires is made very low, we find that at any given moment either nothing arrives, or one and only one—exactly one—bullet arrives at the backstop. Also, the size of the lump certainly does not depend on the rate of firing of the gun. We shall say: “Bullets always arrive in identical lumps.” What we measure with our detector is the probability of arrival of a lump. And we measure the probability as a function of x. The result of such measurements with this apparatus (we have not yet done the experiment, so we are really imagining the result) are plotted in the graph drawn in part (c) of Fig. 37–1. In the graph we plot the probability to the right and x vertically, so that the x-scale fits the diagram of the apparatus. We call the probability P12 because the bullets may have come either through hole 1 or through hole 2. You will not be surprised that P12 is large near the middle of the graph but gets small if x is very large. You may wonder, however, why P12 has its maximum value at x=0. We can understand this fact if we do our experiment again after covering up hole 2, and once more while covering up hole 1. When hole 2 is covered, bullets can pass only through hole 1, and we get the curve marked P1 in part (b) of the figure. As you would expect, the maximum of P1 occurs at the value of x which is on a straight line with the gun and hole 1. When hole 1 is closed, we get the symmetric curve P2 drawn in the figure. P2 is the probability distribution for bullets that pass through hole 2. Comparing parts (b) and (c) of Fig. 37–1, we find the important result that

The probabilities just add together. The effect with both holes open is the sum of the effects with each hole open alone. We shall call this result an observation of “no interference,” for a reason that you will see later. So much for bullets. They come in lumps, and their probability of arrival shows no interference.
 الاكثر قراءة في ميكانيكا الكم
الاكثر قراءة في ميكانيكا الكم
 اخر الاخبار
اخر الاخبار
اخبار العتبة العباسية المقدسة

الآخبار الصحية















 قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة
قسم الشؤون الفكرية يصدر كتاباً يوثق تاريخ السدانة في العتبة العباسية المقدسة "المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة
"المهمة".. إصدار قصصي يوثّق القصص الفائزة في مسابقة فتوى الدفاع المقدسة للقصة القصيرة (نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)
(نوافذ).. إصدار أدبي يوثق القصص الفائزة في مسابقة الإمام العسكري (عليه السلام)


















