في عام 1913 وضع الفيزيائي الدانماركي نيلز بور نموذج متكامل للذرة. لم يكن نموذجه وصف للنواة الذرية، إذ لم يدع رذرفورد أحدا بعده ليتكلم عن النواة الذرية كثيرا في عصره. كان بور قد وضع نموذجه ليفسر خطوط الطيف الذري، ويتجنب الصعوبات التي واجهت نموذج رذرفورد عن الالكترونات. لذلك من الممكن القول بأن نموذج بور للذرة هو نموذج للإلكترون.

وجد بور الحل في تجنب مشكلة السقوط الحلزوني للإلكترون داخل النواة، باستخدام حلال المشاكل، دستور بلانك – اينشتاين. افترض بور للتخلص من الصعوبات النظرية ما يلي:

1. يدور الإلكترون بشكل دائري حول النواة تحت تأثير قوة كولوم، بدون إطلاق أي أشعة كهرومغناطيسية.

2. يتواجد الإلكترون في مدارات محددة حول النواة، ولا يمكن أن يتواجد بينهما. ولما كانت خطوط الطيف تصدر بشكل خطوط متقطعة من التردد الزاوي، يجب أن تكون كمية التحرك الزاوي مكممة أيضا أي تأخذ قيما محددة فقط. تعطى كمية التحرك الزاوية المكممة تلك كالتالي:

 h/2π= ħ، وn عدد صحيح ويأخذ قيما عادية .... ،1،2،3 = n ويسمى بعدد الكم الرئيسي principle quantum number.

3. يصدر الإلكترون عند انتقاله من مدار إلى أخر إشعاعا كهرومغناطيسيا، أو فوتون لكل إلكترون. يعطى تردد كل فوتون بالعلاقة التالية:

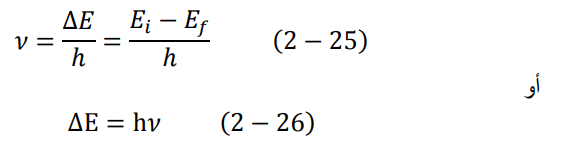
وهنا نرى دستورنا القديم دستور بلانك – اينشتاين.

إن الفرضية الأولى في نموذج بور تنتهك بشكل واضح وصريح تنبؤات النظرية الكهرومغناطيسية، ولكنها تتفق مع قوانين الميكانيكا الكلاسيكية، مثل قوة كولوم وقوانين نيوتن. لذلك استخدم بور قانون كولوم لحساب قوة الجذب الكهربائي بين النواة والإلكترون. تعطى تلك القوة كالتالي:

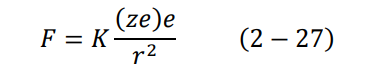
حيث e شحنة الالكترون، وze شحنة النواة طالما أننا نعالج ذرة الهيدروجين هنا وهي أخف الذرات، ستكون 1 = z. وهذا لان ذرة الهيدروجين تحتوي على بروتون واحد فقط. في حالة استقرار الذرة تكون قوة الطرد المركزي مساوية لقوة الجذب الكهربائي. باستخدام قانون نيوتن الثاني نجد أن:

وهي سرعة الالكترون المكممة، ومكممة لأنها تحتوي على العدد الصحيح n. كذلك بالإمكان أن نجد:

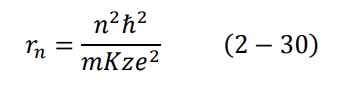
وهو نصف قطر الذرة (بعد الإلكترون عن النواة) في إحدى المدارات.

عندما يكون الإلكترون في مستوى الطاقة الأول، تكون (1 = n) وتتخذ المعادلة (30-2) أصغر قيمة لها، وهو أصغر نصف قطر للذرة، ويسمى نصف قطر بور a_o Boher radius. وعند التعويض في المعادلة (30-2) نجد أن:

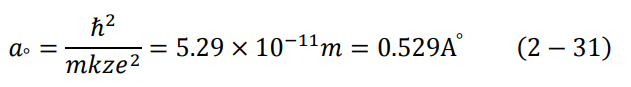
وبالتالي يمكن كتابة المعادلة (30-2) بدلالة نصف قطر بور كالتالي:

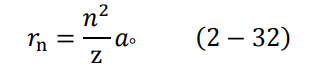
بالمثل نستطيع إيجاد سرعة الإلكترون في المدار الأرضي، وذلك بوضع 1 = n في المعادلة (29-2):

v₁ = 2.19 × 10⁶ m/s

وهذه أكبر قيمة لسرعة الإلكترون في ذرة الهيدروجين. نلاحظ أن هذه السرعة صغيرة جدا بالنسبة لسرعة الضوء، وهذا يعلل إهمال تأثير الميكانيكا النسبية هنا.

نستطيع الآن إيجاد طاقة الإلكترون الكلية E_n في احدى مداراته حول النواة، وذلك من خلال العلاقتين (29-2) و(30-2)، مع استخدام الإشارة السالبة للجهد الكهربائي، لأننا سنعتبر جهد الإلكترون يساوي الصفر عندما يكون على بعد لا نهائي من النواة:

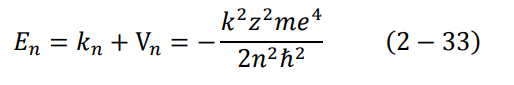
عندما يكون الإلكترون في الحالة الأرضية 1 = n تصبح المعادلة (33-2):

E_n = – 13.6 eV

وهي طاقة الإلكترون الكلية في المدار الأرضي من الممكن كتابة المعادلة (33-2) على النحو التالي:

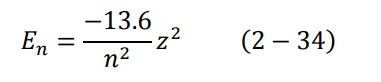
لنفرض الآن أن الإلكترون قد انتقل من مستوى الطاقة  ∞= n الى 1 = n، باستخدام المعادلتين (33–2) و (26–2) مع c/λ = v وأخذ من المعادلة (23–2)، نجد أن المعادلتان لا تتساوى إلا في حالة:

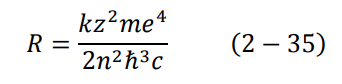
وتساوي هذه الكمية بالضبط ثابت رايد بيرغ!! لكن هذه المرة بدلالة مقادير فيزيائية معروفة تماما.

بهذه الطريقة أعطى بور المعنى الفيزيائي لثابت رايد بيرغ، الذي كان معروفا من قبل كثابت تجريبي فقط. كذلك أصبحت جميع المتسلسلات التي تصف الأطوال الموجية لطيف ذرة الهيدروجين حالة خاصة لنموذج بور، حيث نجد من متسلسلة بالمر، المعادلة (23–2)، تحتوي على العدد 2²، وهذا يعني الآن بحسب نموذج بور انتقال إلكترون من مستوى الطاقة n إلى مستوى الطاقة الثاني، ومن ثم إطلاق فوتون ضوئي. لذلك كان الرقم الصحيح في متسلسلة بالمر لا يأخذ إلا قيما من ثلاثة فصاعدا تفسر جميع المتسلسلات الأخرى بنفس الطريقة بالضبط.

يوضح الشكل (11–2) مستويات الطاقة المختلفة لذرة الهيدروجين حسب نموذج بور. إذا أردنا حساب مستوى أي طاقة، نقوم باستخدام المعادلة (34–2). فمثلا لمعرفة حساب مستوى الطاقة الثاني، نضع 2 = n في المعادلة (34-2):

حيث 1 = z، وهكذا لبقية المستويات.

اعتبرنا في هذه المعالجة أن كتلة النواة (البروتون) كبيرة جدا بالنسبة لكتلة الإلكترون. ففي حالة ذرة الهيدروجين تكون كتلة النواة (البروتون) أكبر من كتلة الإلكترون بـ 1836 مرة. لذلك إذا أردنا تحسين الحسابات بشكل أكثر دقة، نقوم بتعويض ما يسمى بالكتلة المختزلة reduced mass، بدلا من كتلة الالكترون في جميع المعادلات الموجودة في نموذج بور. تعطى الكتلة المختزلة كالتالي:

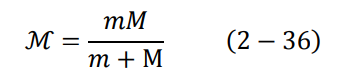
حيث M كتلة البروتون وm كتلة الإلكترون.

إن نموذج بور حول الذرة مقنع للغاية في تفسير خطوط الطيف الذري على الذرات أحادية الإلكترون. ويمكن تطبيقه على بعض الذرات المتأينة، والتي تسمى بالذرات الهيدروجينية. مثل الهيليوم المتأين (He⁺) والليثيوم المضاعف التأين (Li²⁺⁺). في هذه العناصر نقوم بتعويض العدد الذري z الخاص بها في كل المعادلات السابقة.

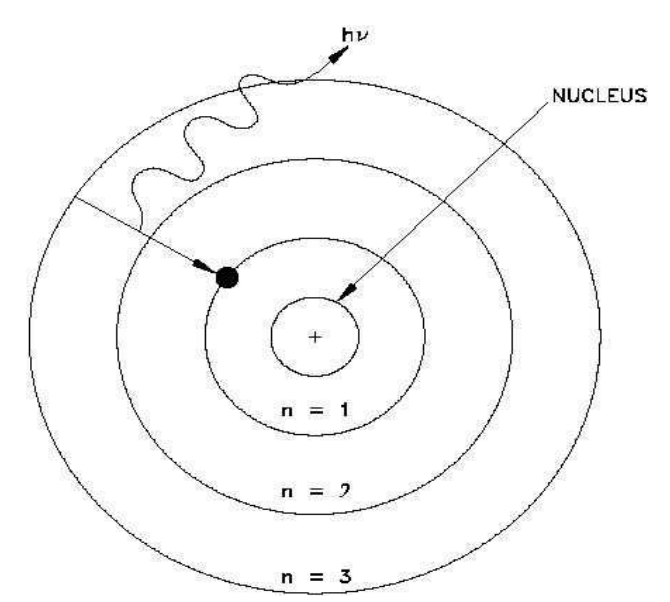
شكل (11–2)

مستويات الطاقة المختلفة لذرة الهيدروجين. صدور فوتون ضوئي طاقته hv عند انتقال الالكترون من مستوى الطاقة الثالث 3 = n الى مستوى الطاقة الأول 1 = n.

بصورة عامة يتوافق نموذج بور مع ذرات العناصر الخفيفة المتأينة التي يكون عددها الذري 20 >> z. أما في حالات العناصر الثقيلة 20 < z فلا تتفق النتائج مع نموذج بور. كذلك في حالة زيادة العدد الذري فأن ذلك يؤدي الى زيادة سرعة الالكترون (انظر المعادلة (29–2))، وهنا يكون تأثير الميكانيكا النسبية مهما.

إذن على الرغم من جمال نموذج بور، إلا أنه لا ينطبق إلا على الذرات وحيدة الإلكترون. ولكن في حالة الذرات المتعددة الإلكترون يفشل النموذج تماما في تفسير خطوط الأطياف الذرية.

مما هو جدير بالذكر ما قام به كل من سومرفيلد وویلسون Sommerfeld & Wilson من تطوير لنموذج بور. حيث افترضا أن مدارات الالكترونات بيضاوية الشكل وليست دائرية، وتقع النواة في إحدى البؤرتين يذكرنا ذلك بنموذج كبلر Kepler حول حركة الكواكب في المجموعة الشمسية جعلت تلك الفرضية مدارات بور حالة خاصة لها إضافة إلى ذلك تم تطبيق الميكانيكا النسبية بدلا من الميكانيكا الكلاسيكية وتم تفسير التشققات التي تحدث لخط الطيف الواحد لكن مع كل ذلك تفشل تلك المعالجات الجديدة بالنهاية في معالجة الذرات المتعددة الالكترونات، كما فشل نموذج بور.