هناك عالم يسود فيه نوع مختلف من النظام غير ما ألفناه في حالة البلورات الحقيقية التي تنتظم فيها الذرات أو المجموعات الذرية مكونة شبيكة ذات ثلاثة أبعاد وتحكمها قوانين هندسية صارمة تؤدي إلى تقسيم البلورات إلى مجموعات نقطية ومجموعات فراغية وغيرها.

لقد مر بنا في الأبواب السابقة أن الترتيب بعيد المدى في بلورة دورية نموذجية ولا نهائية الأبعاد لا يطرأ عليه أي تغيير عندما تحدث إزاحة باتجاه متجهات الانتقال التي سبق تعريفها على أن صفة الدورية هذه ليست بالضرورة من متطلبات النظام بعيد المدى. ولكي تتضح هذه الفكرة دعنا نتناول بنية دورية ذات بعد واحد ولتكن هذه البنية بسيطة غاية البساطة حيث تتكون من نقط يفصل بين كل منها والأخرى مسافات متساوية مكونة بهذا شبيكة ذات بعد واحد.

تعرف كثافة الشبيكة أحادية البعد بالتعبير الرياضي التالي:

حيث «a» هو بارامتر الشبيكة ولا تعدو مركبات «فوريه» لهذا التركيب كونها سلسلة من القمم الحادة التي تعرف برقم صحيح واحد هو h (إحداثي ميلر) طبقا لما يلي:

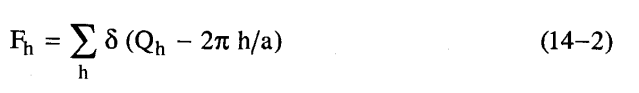
حيث F معامل التركيب وQ هو الفرق بين متجهي الموجة k ، k'.

أما إذا كانت البنية أحادية البعد قد تكونت نتيجة تراكب سلسلتين من النوع الموصوف بالمعادلة (1-14) ولكن البعد التكراري لإحداهما يختلف عن البعد الخاص بالثانية فإن الكثافة تصبح:

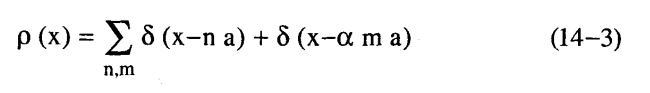
ويظل هذا التركيب متمتعا بنظام بعيد المدى وإن كان غير دوري إذا كانت «α» – وهي النسبة بين البعدين التكراريين – كسرا غير حقيقي.

أي أنه لا يمكن أن يحدث تطابق في الحيز بين مركبتين دوريتين للبنية كلها. ويمكننا فك كل من المركبتين الدوريتين على هيئة سلسلة «فورييه» على نمط المعادلة (2-14). ثم تضاف السلسلتان معا لكي نحصل على مجموعة من مركبات «فورييه» التي تمثل التركيب غير الدوري (3-14) كما يلي:

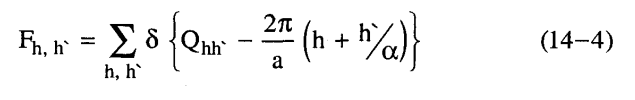
وهنا تعرف F برقمين صحيحين مستقلين هما h، h' على الرغم من أنها ظلت دالة حادة مثلما هو الحال في البنية الدورية. أي أن الفراغ المقلوب بالنسبة للكثافة (ρ(x (المعادلة (3-14)) قد يظل فكرة مثيرة للاهتمام، ولكن الكثافة في هذا الفراغ المقلوب، أكبر من تلك التي لبنية دورية معتادة، بل وقد تكون كبيرة جدا؛ لأن مضاعفات الكسر غير الحقيقي α سوف تغطي الوحدة الأساسية بشكل مكثف.

يمكننا – على أية حال – بناء أية بنية غير دورية وذات ترتيب بعيد المدى باستخدام أي أسلوب غير عشوائي يتيح لنا في النهاية إنشاء نسق ذري. ومن أمثلة ذلك سلسلة «فيبوناتشي» ذات البعد الواحد. هناك العديد من الطرق المتبعة للحصول على هذه السلسلة ذات الفترات المتعاقبة. ومن هذه الطرق ما يبدأ بتتابع محدد مكون من مقطعين أحدهما قصير «S» والآخر طويل «L» ويتم الاستطراد بمبدأ التكرارية S→L و L→LS حتى تتكون أوتار متعاقبة ذات أطوال آخذة في الزيادة، ومثال ذلك ما يلي:

فإذا كانت النسبة 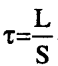رقما غير جذري (كسر غير حقيقي) فإن التتابع لا يكون ذا مسافة تكرارية وعندئذ ينتمى تتابع «فيبوناتشي» القانوني للكمية 36º = 2 cos τ أو ما يساوى 1.618034 وهو الذي يعرف بالمتوسط الذهبي Golden Mean ويلعب دورا مهما في مجال تماثل المجسمات ذات العشرين وجها؛ من المركز إلى رأس خماسي الأضلاع والمسافة من المركز إلى المسافة فالنسبة بين منتصف الحافة تساوي 2/τ

ويعتبر نمط الحيود الخاص ببنية «فيبوناتشي» ذا أهمية بين باقي الأنماط نظرا لأنه يتكون من مجموعة من القمم المعروفة بقمم «براج» التي تتكدس لتملأ الفراغ المقلوب. فإذا اعتبرنا المواقع الذرية خاضعة للتعبير التالي:

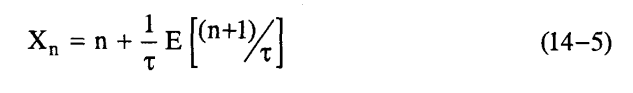
وهو يناظر سلسلة «فيبوناتشي» إذا اعتبرنا أن طول المقطع يساوى (1 وτ). فالحد الأول بمفرده يساوى واحد (1)، أما الحد الثاني فيكون متزايدا بمقدار /τ1 في كل مرة تزداد فيها n بمقدار τ وعلى هذا يمكن تقسيم X_n إلى مجموع دالتين تصنعان مسافة دورية، وإن كانت تلك الدورات غير متناسبة incommensurate بشكل يشبه إلى حد ما تمثله المعادلة (3-14). ولو أننا احتفظنا بالحد الأول فقط لأصبح نمط الحيود مكونا من قمم «براج» يفصل بين بعضها البعض في الفراغ المقلوب مسافات دورية، ومقدار الدورة الأساسية هو Q₁. وحيث إن الحد الثاني غير متناسب فإنه بقود من ثم إلى قمم (براج) ذات الدورة Q₂ غير المتناسبة في الفراغ المقلوب.

أي أن النمط بأسره سيتكون من اتحاد مجموعتين من القمم، بالإضافة إلى ائتلاف خطي مكون من Q₁ ، Q₂. وحيث إن كلتيهما غير متناسبة؛ لذا فإن القمم ستتكدس في الفراغ المقلوب.